第十六篇 电化学阻抗谱(EIS)-(6)
Laboratory Of Research & Development, BAS Inc.
Professor Noriyuki Watanabe
Professor Noriyuki Watanabe
半圆的直径与每个并联电路的电阻值R匹配。 电阻为100Ω的过程对应于最大的圆弧。时间常数是10-2秒,它出现在最低频率侧,反映了最长的基本过程(正如之前提到的,在奈奎斯特图中越接近原点处的频率越高,越远离原点处的频率越低)。
在图16-1 中,5×10-6秒的基本过程出现在最高频率侧,反映了最短的时间常数,并对应于具有最小并联电阻的过程。中间的圆弧与时间常数为10-4秒的基本过程相对应。 使用等式fmax = 1 /2ΠCR从半圆的峰值频率(fmax)和电阻值R可获得电容C的值。
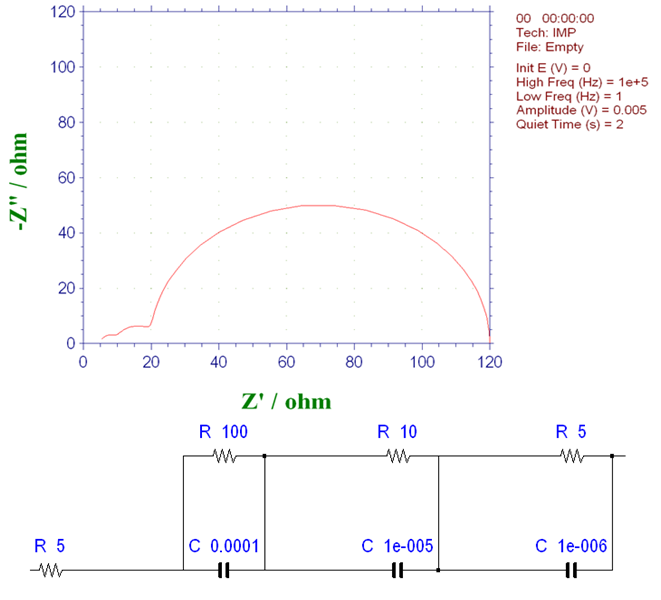
图16-1 含三个连续发生的基本过程体系的奈奎斯特图 (1)
在寻找这些等效电路的过程中,必须考虑等效电路是否适当地对应于实际的化学和物理现象。从这个意义上讲,电阻,电容和Warburg阻抗很容易考虑。
例如,电阻反映了介质本身的电阻,界面处的电荷传递速率以及溶液,薄膜和各种其他介质中离子传输速率的大小。如果电极上的电子传递速率较慢,则对应于较大电阻。 由于极性界面的形成,电荷的充电/放电等形成了电容。
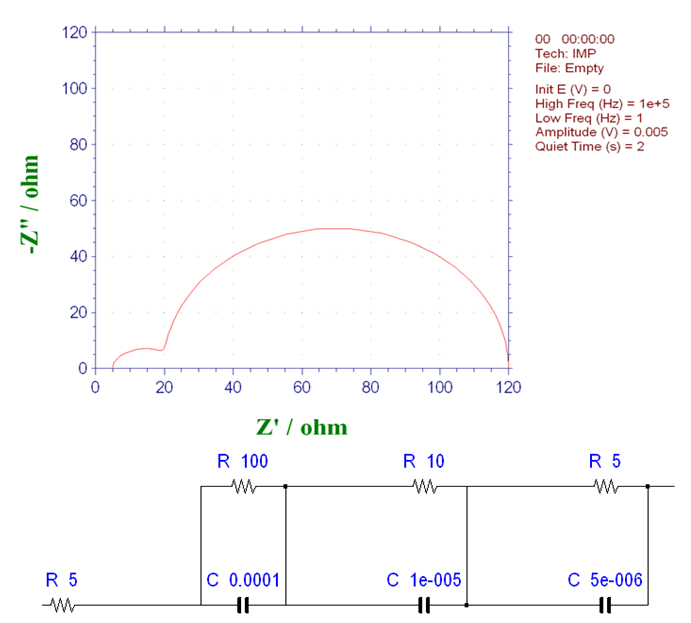
图16-2 含三个连续发生的基本过程体系的奈奎斯特图 (2)
此外,在各种涉及扩散的现象中都会出现沃伯格(Warburg)一词。 幸好这些现象的时间常数具有经验累积或可以粗略地估算出来。 另一方面,对于CPE,我们可以通过模拟构建一个与测量结果相适应的模型,并得到结果。 但在数学上,根据n的选择,其模型可以是电容、电阻或电感,因此必须认识到仅从这些是很难描述其化学现象或物理现象。
