基础电化学测量技术介绍
- 第一篇:循环伏安法测量技术介绍(I)
- 第二篇:循环伏安法测量技术介绍(II)
- 第三篇:循环伏安法测量技术介绍(III)
- 第四篇:循环伏安法测量技术介绍(IV)
- 第五篇:电位阶跃技术(CA,CC,STEP)
- 第六篇:脉冲技术-阶梯波伏安法(SCV)
- 第七篇:常规脉冲伏安法(NPV)
- 第八篇:差分脉冲伏安法(DPV)
- 第九篇:方波伏安法(OSWV)
- 第十篇:交流(AC)技术(ACV、SHACV)
- 第十一篇:流体动力学技术(HDM)
- 第十二篇:电流测量技术(i-t、DPA)
- 第十三篇:双微分脉冲电流法(DDPA)
- 第十四篇:三重脉冲电流法(TPA)
- 第十五篇:积分脉冲电流检测 (IPAD)
- 第十六篇:整体电解法(BE)
- 第十七篇:阻抗测量(IMP)
- 第十八篇:阻抗时间法(IMPT)
- 第十九篇:阻抗电位法(IMPE)
- 第二十篇:计时电位法(CP)
- 第二十一篇:计时电位斜坡电流法(CPCR)
- 第二十二篇:扫描步进功能 (SSF)
- 第二十三篇:多电位阶跃法(STEP)& 多电流阶跃法(ISTEP)
- 第二十四篇:电位剥离分析 (PSA)
循环伏安法测量技术介绍(I)
M.Sc. Takayuki Tezuka
1 电势扫描方法(变动电势法)
电势扫描方法是通过一定的速度改变施加到工作电极上的电势(印加电势)来测量电极反应电流随时间变化(称为“电位扫描”或“电位扫描”)的方法。仅仅沿着一个方向进行电势扫描的方法称为线性扫描电势法(Linear Sweep Voltametry)LSV。如果电势沿一定方向进行扫描后,改变电势扫描的方向进行逆向电势扫描,或者进一步重复这种正反向电势扫描的方法称为循环伏安法。 测量结果通常是用两个随时间变化的参数(电流,电电势)组成的电流 – 电势曲线(伏安图)来表示。 此时,伏安法的响应电流表示对电极反应的施加电位的响应,并且与计时电流法一样,显示了电极反应随时间的响应。

图1-1 循环伏安法
2 三电极电化学测量体系和电流的方向
如图2.1所示, 在这种伏安技术中,基本上是将三种类型的电极连接到恒电位仪上,恒电位仪以参比电极电势为参考基准来控制工作电极的电极电势大小,同时检测在工作电极和对电极之间流过的电流的大小来完成测量。 当在工作电极表面上发生氧化反应时,反应物分子失去的电子可通过连接在恒电位仪上的外部电路从工作电极流向对电极,也就是说,电流的流动方向是从对电极流向工作电极的。

图2-1 恒电位仪和三电极体系连接示意图
循环伏安法测量技术介绍(II)
M.Sc. Takayuki Tezuka
3. 电流-电势曲线
作为典型的循环伏安法测量的一个例子,让我们看一下含有铁氰化物离子(2 mmol / L铁氰化钾+ 1 mol / L硝酸钾溶液)的溶液的电流 - 电势曲线。 在该单电子氧化还原反应中,Fe(CN)63−为氧化态物质, 亚铁氰化物离子Fe(CN)64−为还原态物质。

使用银-氯化银参比电极时,在工作电极上所施加电势的时间变化在图3-1中表示。施加在工作电极上的电势以100mV / s的扫描速率从0.6 V 向-0.1V 进行负方向(还原方向)扫描。然后在-0.1V处折回进行反向扫描。电势沿负方向扫描开始时,伴随还原反应的电流(该图中的符号为负)流出,并且在0.229V处,还原电流达到峰值。然后扫描电势在-0.1 V处折回进行反向扫描,电势在0.1 V氧化反应开始,在0.289 V处可以观察到で氧化电流峰值。氧化峰电势和还原峰电势之间的差异称为峰值电位差,并且该值在25°C时接近0.059 / n V(59 / n mV)。 注意,n是反应电子转移数。 但是,该等式仅适用于电荷转移速度快的情况。
测得的伏安图在图3-2中表示。在测量开始时大约为0A的电流开始在向负方向扫描电位的第一步中流动,并且减小的电流(该图中的符号为负)流出,达到0.229V的减小峰值。此时观察到的电流称为还原峰值电流。之后,电位扫描方向返回-0.1 V,亚铁氰化物离子的氧化开始于0.1 V左右,在0.289 V处观察到氧化峰。氧化峰电位和还原峰电位之间的差异称为峰值电势差,并且该值在25°C接近0.059 / n V(59 / n mV)。注意,n 是反应电子的数。但是,该公式仅适用于电荷转移速度快的情况。

上式中的: ΔE是氧化还原峰电势差, Epa是氧化峰值电势,
Epc是还原峰值电势,n 是转移电子数。
两个峰值电势之间的中间电势(中点电势) Em (0.259 V) 接近于标准电极电势Eo, 因为氧化态和还原态的扩散速率(扩散系数)没有差别。 因此,循环伏安法通常可用于估测近似标准电极电位' Eo。
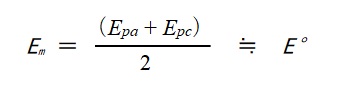
上式中的: Em 是中点电势, Epa 氧化峰值电势,
Epc 是还原峰电势,以及E0 是标准氧化还原电势


图 3-1 扫描电势随时间变化 图 3-2 循环伏安图
循环伏安法测量技术介绍(III)
M.Sc. Takayuki Tezuka
4 峰电流
电流峰顶点处的法拉第电流称为峰电流,对于快速电子转移的可逆反应体系,其峰电流的大小可以用以下的公式(Randles-Sevcik公式)来表示。
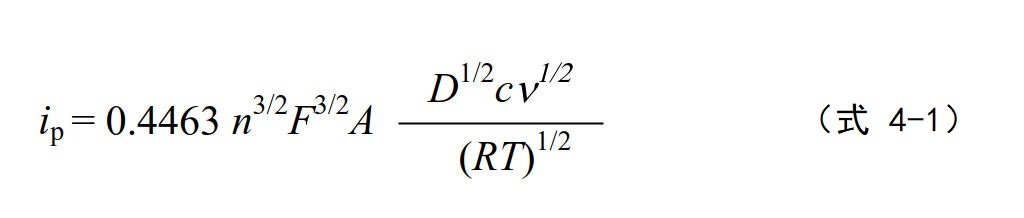
式4-1 中各个参数名称及其单位 ip 峰电流(A), F :法拉第常数 (96485 C/mol),A:工作电极面积 , D:扩散系数,
c:浓度:(mol L-1 ), ν:电势扫描速度(V s-1) , R:理想气体常数 (8.31 J・K-1・mol-1), T:绝对温度 (K)
在25°C时,将上式中的各常数合并后可以简化表示成下面的式子:
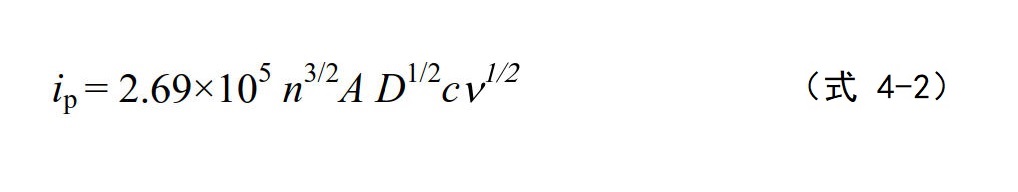
因此,峰值电流与氧化还原物质的电极径向表面浓度c,以及扫描速率的平方根成正比。
图4-1显示了2 mmol / L铁氰化钾溶液在扫描速率分别为0.01, 0.04 和 0.09 V / s时的循环伏安测量结果。 图4-2显示了扫描速率的平方根与还原峰值电流之间的关系,可以看出存在线性关系。 您还可以通过绘制此图的近似线并使用其斜率来求得扩散系数D等参数。
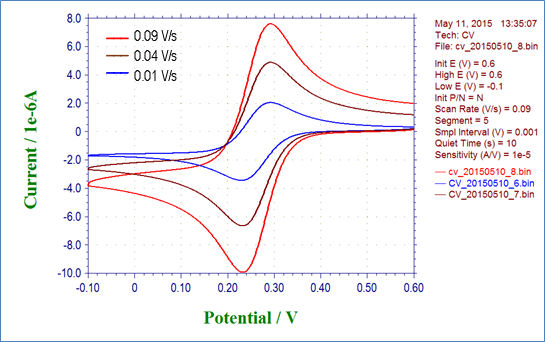
图 4-1 不同扫描速率下测得的 2 mmol/L K3Fe(CN)6 循环伏安图.
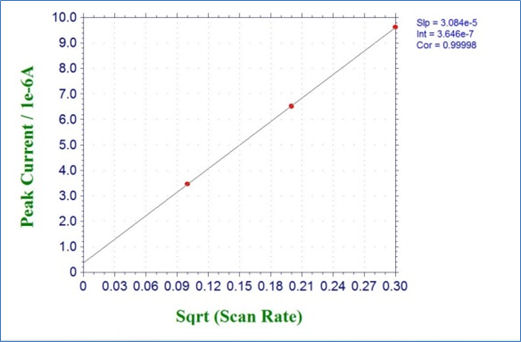
图 4-2 还原 峰值电流与扫描速率的平方根的曲线图.
循环伏安法测量技术介绍(IV)
M.Sc. Takayuki Tezuka
5 法拉第电流和充电电流
在循环伏安法测量得到的电流中,除了基于氧化和还原反应产生的法拉第电流成分之外,还有因在电极界面上形成的双电层的充电和放电引起的非法拉第电流。 这部分非法拉第电流可通过对不含氧化还原物质的电解质溶液的循环伏安电势扫描测量(背景测量),并扣除背景电流后,即可得到校正。
图5.1是测得的循环伏安曲线(红线),背景曲线(棕色线)和背景扣除校正后的曲线(蓝线)的叠加图。

图5.1 循环伏安曲线(红线),背景曲线(棕色线)和背景扣除校正后的曲线(蓝线)
6. 准可逆和不可逆系统的伏安法测量
在电极界面上慢速电子转移的电化学反应系统被称为不可逆系统。 可根据反应速度常数k0 的大小来区分(n是反应电子数)
可逆系: k0 > 0.3(nv)1/2
準可逆系: 2 x 10-5 (nv)1/2 < k0 < 0.3(nv)1/2
非可逆系: k0 < 2 x 10-5 (nv)1/2
图6.1是使用模拟软件来改变循反应速率k0 得到的准可逆系统的伏安图。 在这些伏安图中,尽管氧化-还原峰值电势差变大,但如果在氧化侧和还原侧扩大程度几乎相同的话,则中点电位 Em可用于估计标准电极电位E0 。 另一方面,如果没有出现两个明显的电流峰,则难以通过中点电位Em估计标准电极电位E0 。

图6.1 在不同反应速度下循环伏安图的变化(模拟图)
电位阶跃技术(CA,CC,STEP)
这些技术是将电位从一个值改变为第二个值,并记录电流(计时电流法)或电荷(计时电流法)作为时间的函数(电荷是电流的积分)。在将第二电位保持一段时间τ之后,该电位将更改为第三值(通常是初始电位值)。因此,电位阶跃实验可以是单阶跃或双阶跃。计时电流法和计时电量法(即计时库仑法)的一般变量略有不同。
计时电流法需要一个初始电位(初始电位E)和一个高电位和一个低电位。将电位从初始电位更改为低电位或高电为(这由初始P / N变量确定)。在经过时间τ(脉冲宽度)之后,电位沿相反的方向变化(从低电位到高电为,或从高电位到低电位)并保持τ时间(见图1)。对于计时电量法,电位是初始电位(初始电位E)和最终电势(最终E)(见图2)。

图1计时电流法电位波形

图2 计时电量法电位波形
由扩散支配而产生的法拉第电流在t-1/2处衰减(典型计时电流图,见图3)。

图3 计时电流图(电流-时间应答)

图4 计时电量图(电荷量-时间应答)
CA和CC测量用于使用线性图的直线斜率来确定n,C,A,D中的一个。 但是,必须知道四个参数中的三个。 但是,其他技术(例如,以后将要介绍的脉冲技术)具有较低的检测极限,因此CA和CC一般不会用于浓度测量。 通常使用这些技术来测量A和D。
i与t-1/2或Q与t1/2之间的关系用于确定通过扩散严格控制电流(或电荷)的时间间隔。 图5是i 与t-1/2之间的关系图。 短时间内与理论值的偏差取决于向工作电极充电的阶跃电位所需的时间长度。 长时间与理论值的偏差是由于自然对流引起的。

图5 电化学体系中平面扩散条件下的时间窗口的的示意图,i /t-1/2(CA)图。
如果印加的最终电位值不能发生快速电子转移,那么电流(或电荷量)响应将会和扩散速度同样,会受到电子转移速度不均匀的影响。 因此,可以通过CA和CC来测量电子传递速率。
与CA相比,CC具有多个优点。 信号随时间增加。 响应的后半部分不会因开始时集中的充电电流而失真,因此可以获得良好的S/N信噪比。 另外,在电荷量在实验过程进行累计,因此初始响应的信息也会被保留。
CC的另一个应用是利用其保留初始信息的能力,检测吸附在工作电极表面的物质。 这类物质一旦电位改变,就会很快被电解。在测时过程中测量的总电荷量为
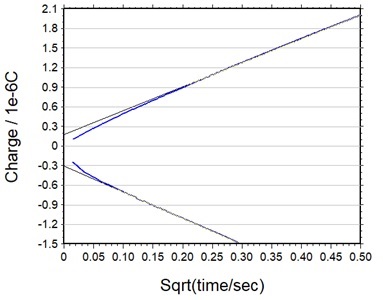
图6 正向/反向Anson图。
脉冲技术
线性扫描技术的缺点之一是存在反向电流(电容电流)。因此,使用这些技术来进行浓度定量测量并不是一个好方法。
检测极限会受到背景电流的影响。
• 脉冲技术的重要变量是:
o a. 脉冲幅度是电位脉冲的高度,以mV为单位显示。
o b. 脉冲宽度是电位脉冲的持续时间,以毫秒为单位显示。
o c. 采样宽度是指测量电流的脉冲的经过时间(毫秒)。
它必须至少比脉冲宽度短3 msec(3毫秒是电容电流衰减到零所需的时间)。对电流进行采样,平均每毫秒16次。 采样时间的默认值为17msec。 也就是说,这是一个商业电源(60Hz)的一个周期的时间(所以线路噪声平均为零)。
o d. 脉冲间隔/滴落时间-这是一个电位周期(msec)所需的时间,
并且必须至少是脉冲宽度的两倍。脉冲间隔用于伏安法实验,
滴落时间用于极谱法实验,电势脉冲,电流采样和汞滴的滴落是相互关联的。
下面介绍三种不同电位脉冲波形和采样次数的脉冲技术。 消除背景电流的能力,提高灵敏度和较低的检测极限(与线性扫描技术相比),使这些方法成为浓度定量的理想技术。
阶梯波伏安法(SCV)
直流极谱实验的改良版本,旨在减少汞滴表面积变化的影响。电位波形如图6-1所示。电位以恒定的步长变化(与滴落时间周期完全同步)。 在每次滴落结束时对电流进行采样。 滴落时间和步长大小可以设置为各种数值。这种电位波形还可被称为阶梯波形。

图6-1 SCV电位波形

图6-2 典型的SCV电流响应
id= 708nD1/2Cm2/3τ1/6
n =电子转移数/ mol
D =扩散系数(cm2/s)
C =浓度(mol/cm3)
m =汞流速(mg/s)
τ=采样间隔
SCV的灵敏度和检测极限类似于直流极谱法(5 µA / mM,10&sup(-5)M)。SCV相对于直流极谱法的主要优势在于其平滑的电流输出,这使得测量半波电势和法拉第电流变得容易。这本质上是一种极谱技术,但可以用作低扫描速度伏安法技术。这种改进的版本称为阶梯伏安法。
常规脉冲伏安法(NPV)
脉冲技术的电势波形如图7-1所示。它由一系列具有增加的电势和振幅的脉冲组成,这些脉冲在脉冲之间返回到其初始值。如果初始电势相对于氧化还原电势足够正(在考虑氧化剂的还原反应时),则当施加小幅度脉冲时,不会发生法拉第反应,并且没有电流响应。当脉冲幅度大到足以使脉冲电势接近氧化还原电势时,就会发生脉冲对应的法拉第反应(假定电子传输速率适度快)。而且该法拉第电流的大小取决于扩散速率和电子传输速率。
当脉冲电势相对于氧化还原电势变得足够负并且电子传输发生得更快时,法拉第电流变得仅取决于扩散速率。即,达到极限电流。
该电流响应如图7-2所示。S形波形类似于经典极谱实验中获得的波形曲线。这就是为什么我们将此方法称为常规脉冲方法(类似于HPLC的正相,反相,正相和突增相,历史上较旧的方法称为正相)。NPV法拉第电流比SCV大,技术更灵敏(30 µA / mM),检测下限较低(10-6 M)。

图7-1 NPV/P 电位波形

图7-2 典型的NPV / P电流响应
差分脉冲伏安法(DPV)
DPV技术与前两种技术的不同之处在于,每个脉冲间隔对电流采样两次。图8-1显示了时间的函数和作为电流采样方法印加的电位波形。
在差分脉冲伏安法(DPV)中,施加恒定振幅的脉冲电位,基础电位从初始电位开始朝着最终电位进行小幅增加。即,将具有小幅度的脉冲叠加在线性增加的阶梯波形上。在脉冲(i 1)之前和脉冲(i 2)结束时对电流进行采样。记录差(i 2 -i 1)作为基础电位的函数。以还原为例,在相对于Redrex电势足够正的电势下不会发生电极反应,并且电流差为零。电流差在氧化还原电位附近达到最大值,并且当控制扩散速率时,电流差再次减小到零。在NPV中,将初始电位设置为不发生法拉第反应的电位值。

图8-1 DPV的电位波形

图8-2 DPV的典型电流响应
方波伏安法(Osteryoung square wave voltammetry) 与脉冲技术和交流伏安技术密切相关。与 DPV/P 类似,它们给出了一个峰形电流响应曲线,并有效地消除了背景电容电流。主要优点是灵敏度高、速度快。

图9-1 OSWV的电位波形
默认的电流输出是作为差值电流给出的(图 9-2 ),但正向(if)和反向(ir)电流也是单独确定的(图9-3)。
在可逆系统中,反向电流也较大,所以差值电流比正向或反向电流都大。 这就是OSWV比DPV更敏感的原因之一。 反向电流的大小被用来研究电子转移的可逆性。

图9-2 OSWV的差分电流响应
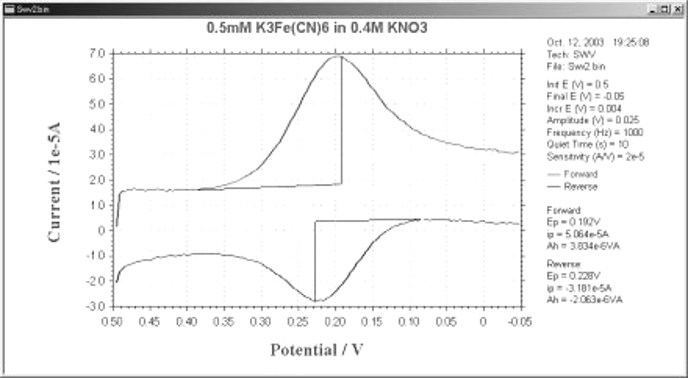
图9-3 OSWV 正向和反向电流响应
交流(AC)技术(ACV、SHACV)

图 10-1 AC阻抗电位波形

图 10-2 SHACV 电位波形
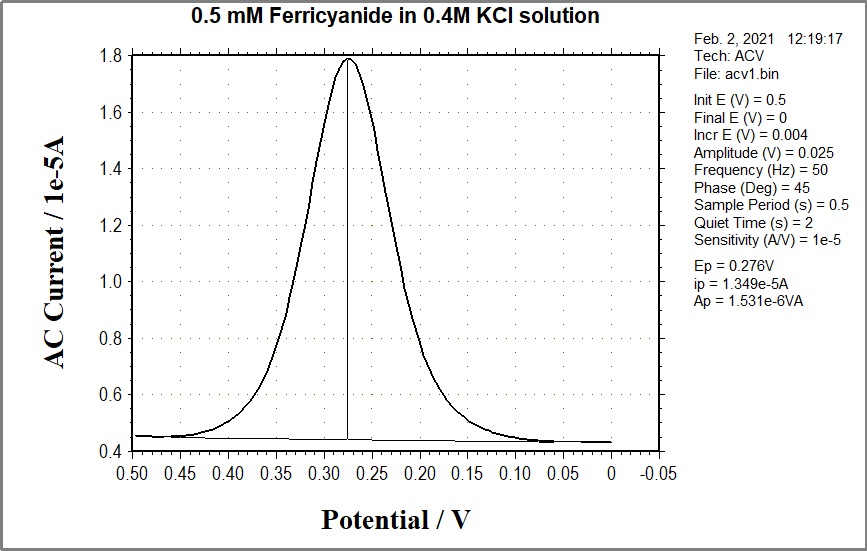
图 10-3 典型的 ACV 电流响应

n = 电子转移数,F = 法拉第常数(96500 C/eq),A = 电极表面积(cm2), ω=2n x (交流频率),
D = 扩散系数(cm2/s),C =浓度 (mol/cm3 ), ΔE=AC 电位振幅
也就是说,它是基波及其谐波的总和。经常使用二次谐波(second Harmonic SHACV/P)频率响应。这种技术获得的信息与ACV/P和PSACV/P相同。此外,消除电容电流更有效,时间尺度更短。SHACV 已被用于测量电解时快速反应的物质的氧化还原电位。(由于SHACV的时间尺度比循环伏安法的时间尺度短,电荷转移后发生的化学反应的影响减小。)图10-4 显示了SHACV的典型例子。
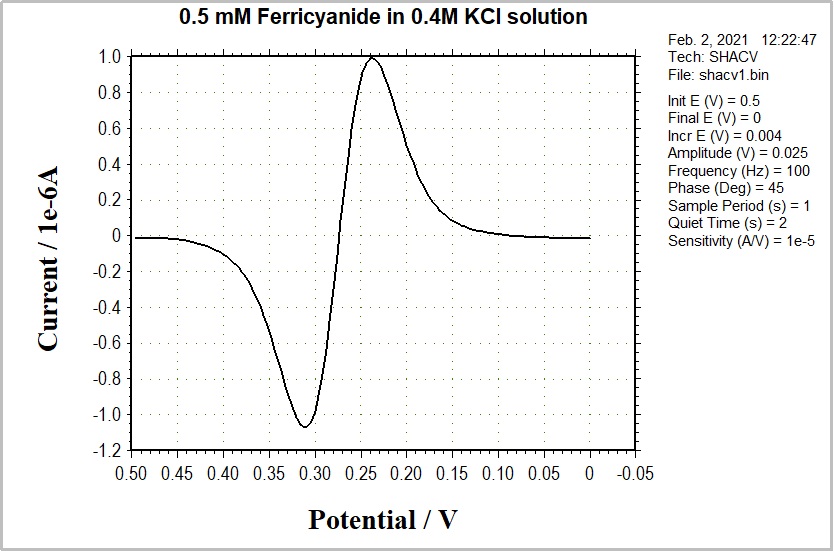
图 10-4 典型的 SHACV 电流响应
流体动力学技术(HDM)
电流对外加电位的响应由许多因素决定。 其中最重要的两点是电子转移速度和从本体溶液到工作电极表面的物质转移速度。 传质方式可分为三种。
i.扩散-由于浓度梯度引起的分子运动
ii.电泳-由于电位梯度引起的分子运动
iii.iii. 对流-由振动和搅拌等干扰引起的分子运动
为了从伏安实验中获得定量数据,重要的是将传质模式定义为易于数学分析的形式。 通过添加充分解离的电解液,可以忽略所有伏安试验中的电泳效应。 体系的传质方式主要由扩散和对流组成。 在许多伏安试验中,通过在不搅拌溶液的情况下防止外部振动来消除对流(这些条件仅保持相对较短的时间)。
使用静态溶液状态的伏安法包括循环伏安法(CV),计时伏安法,脉冲和方波技术。 除了维持无对流条件的实验困难外,以扩散为主的实验还受到缺乏改变传质速率的方法的限制。
在流体动力学技术中,分子以明确定义的方式传输到电极表面。 即通过搅拌溶液,或者如在液相色谱/电化学检测系统中那样通过泵传送溶液通过流动池。 最普遍采用的方法是使用旋转圆盘电极来旋转电极。 由于进入和离开电极表面的传质速率增加,流体力学技术比静态溶液技术具有许多优点。 由于传质和电子转移之间的平衡,更快的传质速率可以更迅速地达到稳态,当扫描速率足够慢时(通常约为20 mV / s或更小),则可以保持稳态。
稳态伏安法的一个优点是在给定的电位下,电流既不依赖于扫描方向,也不依赖于时间。 在这种情况下,伏安图的特征表现为S形曲线。 快速的传质提高了定量分析的灵敏度。旋转圆盘电极常用于剥离实验的析出步骤。 可逆过程的极限电流(传质电流)由Levich方程给出。
n = 电子转移数/mole、F = 电子转移数 (96,500 C/mole)、A = 电极面积(cm2)
C = 浓度(mole/cm3 )、D = 扩散系数(cm2/s)、ω=2 πf ((转数)/rps)、ν= 动态粘度
此kinetic current是从反向Levich图(l/iL对ω1/2)的截距中得出的。 这种方法经常被用于腐蚀和电池的研究。 它还用于测量电子通过覆盖在电极表面上的聚合物膜的移动速度。

图 11-1 HDM外加电位波形
根据Levich公式,l/iL=K ω1/2,其中ω1/2=ωo1/2+ Δω1/2σ t ; ((ωo在中心转速下,频率为σ ,振幅为Δω1/2的正弦波调制,见图11-2),交流电输出如图11-3所示,Δi由下式给出。
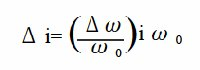

图11-2 利用HDM技术调制转速

图11-3 HDM的交流电输出
电流测量技术(i-t, DPA)
将电流作为时间的函数来测量的这些技术均属计时电流法技术。通常,此类技术用于电流滴定、电流传感器、流动池等的测量。
可应用的三种电化学测量技术(CA, i-t, DPA)之间的区别在于各自所使用的电位波形。即通过设计电位波形以提高选择性。最简单的电位波形是固定电位法,即TB 波形(i-t curve)。TB的电位波形和典型的电流响应分别如图12-1 和图12-2所示。
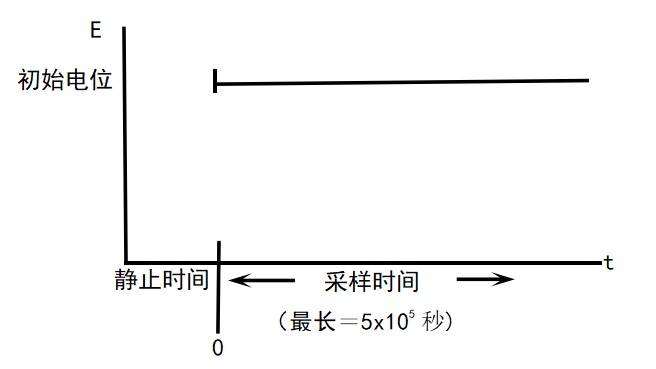
图12-1 TB 的印加电位波形
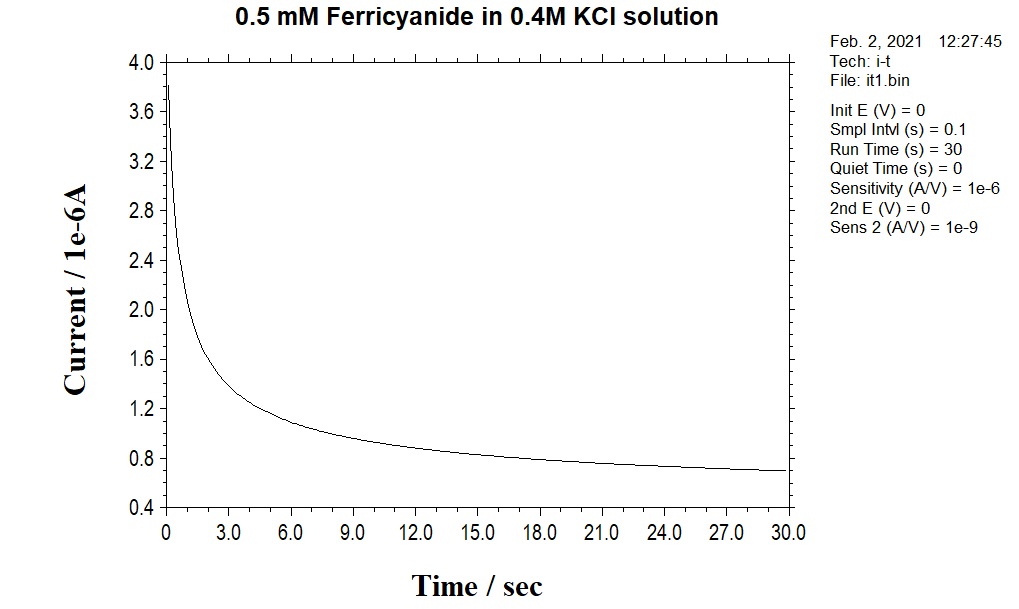
图 12-2 TB 的典型电流响应
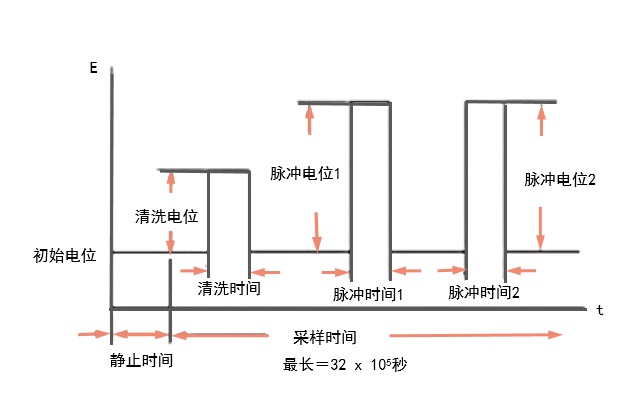
图12-3 DPA 电位波形

图12-4 DPA 的典型电流响应
双微分脉冲电流法(DDPA)
双微分脉冲电流法是通过组合两组微分脉冲电流法来进行的。记录并显示两组数据。每组包括一个无电流采样的清洁电位和两个带电流采样的脉冲电位。
每个脉冲结束时的电流被记录为时间的函数。在实验过程中,仅显示两个电流采样之间的差异。在实验结束时,可以显示两个电位脉冲的电流响应。施加电位波形作为时间和电流采样方式的函数(参见图 31)。

图13-1 电位波形为时间和电流采样方式的函数
可绘制的时间-电流数据类型有
Difference 1 (微分脉冲电流1 vs.时间)
Difference 2 (微分脉冲电流2 vs.时间)
Difference 1 & 2
Forward 1
Reverse 1
Forward and Reverse 1
Forward 2
Reverse 2
Forward and Reverse 2
Forward and Reverse 1 & 2
三重脉冲电流法(TPA)
在简单的电流分析法中,还原糖、伯胺和硫醇的检测需要施加高电位,这样会降低灵敏度和选择性。
三重脉冲电位波形 (TPA) 特别适用于这些分子。顾名思义,连续施加三个电位脉冲,并在每个脉冲结束时对电流进行采样。(图 14-1)此波形重复所需的周期数,将采集的电流数据样本之一显示为时间的函数。(另外两个进行保存,以便后续处理。)
对于糖检测,脉冲序列为:
第一个脉冲清洁电极表面,第二个脉冲在表面形成氧化层,并可能将目标分子吸附到电极上。然后,这些分子被第三个脉冲检测到。由于这是一种特殊情况,因此应将 TPA 视为可用于许多电化学传感器应用的通用波形。
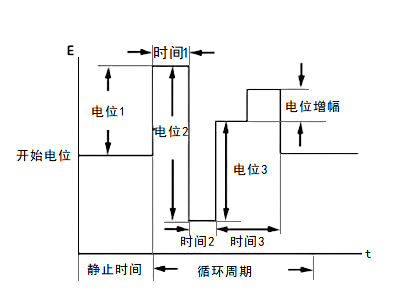
图14-1 TPA 电位波形
积分脉冲电流检测(IPAD)
6段电位扫描或步进法可应用于积分脉冲电流检测。在前四个电位段之间对电流进行采样和积分。最后两个电位步进步骤用于电极处理和清洁。积分电流被平均化并记录为时间函数。下图中的电位波形显示了时间,和电流采样方式的函数。
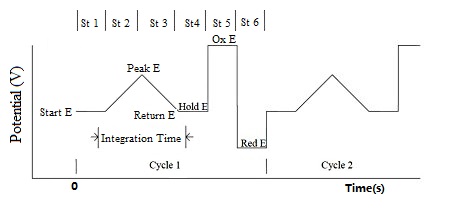
图15-1 IPAD 电位波形
整体电解法(BE)
整体电解(BE)的原理非常简单。如果在电解开始时间仅有氧化态的物质分子存在,可以将电位设置在足够快速还原的负值并保持该电位值,直到溶液中只有还原态的物质。根据法拉第定律,在BE实验过程中通过的总的电荷量 (Q) 与最初存在的氧化态子物质分子的摩尔数 (N) 以及单个分子的电子转移数 (n) 有关。其中 F 是法拉第常数 (96,500C / mol)。因此,如果 n 或 N 的其中一个已知,则可以计算出另一个的值。BE法可以应用于分析和合成的两个方向。
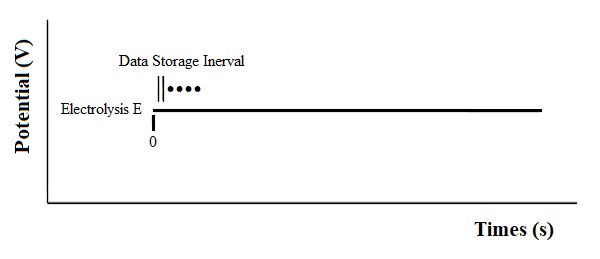
图16-1 BE 电位波形
搅拌溶液可以增加工作电极上物质分子进出的传质速率。应尽量将对电极与工作电极隔离,以防止对电极上的电解产物对工作电极上的电解产物产生干扰。应注意选择用于工作电极与对电极间的隔离材料。如果使用了电阻高的隔离材料,会影响电解效率。
在 BE 实验之前需要选定电解电位。对于还原反应,理想电位应该在氧化还原电位的-200 mV(例如通过循环伏安法测量)处设定。电解速率取决于工作电极上的传质速率。但是,如果其他电化学活性物质(例如,电解液、溶剂和溶液中的其他成分)的电解电位比较近的话,则可能无法使用离氧化还原电位太远的电位。
在 BE 实验过程中,控制软件显示窗口上将显示实验时间。对于每个数据采集时间间隔,在此期间通过的电流和到该点的总电量都显示在软件显示窗口上。还会显示每个采样间隔与第一个采样间隔的平均电流比值。该电流比值是确定电解程度的重要标准。也就是说当该比值达到1%(剩余电流,即背景电流)时,一般认为电解已经完成。最终的电流比例(默认值为1%)也可由用户按需设置。图16-2和图16-3分别为电荷与时间关系,电流与时间关系的结果图。
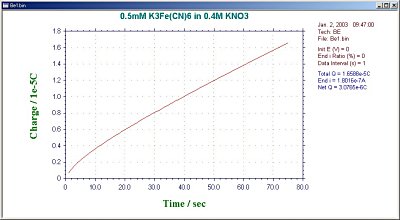
图16-2 典型的BE电荷与时间关系图

图16-3 典型的BE电流与时间关系图
阻抗测量(IMP)
伏安法是在在指定范围内改变电位并监测电流信号响应。对于每次伏安法测量,测量过程中某一时间尺度相关的参数应保持不变(例如,扫描速度)。
在 IMP(阻抗测量) 实验中,初始电位被固定在一个特定的值(例如平衡电位),并在此电位上再叠加一个小幅度的交流电位。每次在一定的交流频率范围的IMP 测量实验,可用于检测具有不同时间尺度的电化学过程和其他物理过程。
傅里叶变换方法被用于波形生成和数据分析。 在交流波的频率范围中,一个频率,以及与这些频率的比例相同且振幅相等,但相位不规则的许多频率被选择使用(图17-1)。结果,创建了一组间隔相对均匀且其频率不是彼此的整数倍的频率。
这组频率被转换为时间范围内波形的数字显示,并通过 D/A 转换器和模拟滤波器应用于测量池。此过程重复多次以提高信噪比。在高频范围内,循环时间相对较短,可以在不增加实验时间的情况下进行多次积分。

图17-1 交流阻抗测量的电位-时间波形
图 17-1 显示了 Z(总阻抗)、Z'(和外加电压同相位的阻抗)、Z"(与外加电压 90° 相位的阻抗)和 θ(相位角)之间的关系。这些变量如图17-2 所示。请注意,它们会随频率 (ω) 的变化而变化。

图 17-2 阻抗 Z 的矢量图
可用于绘图的数据类型
1.Nyquist: -Z"-Z'
2.Bode: LogZ & phase - Log(Freq)
3.LogZ - Log(Freq)
4.phase - Log(Freq)
5.log(Z’& Z”) - Log(Freq)
6.logY - log(Freq)
7.Admittance: Y”- Y’
8.Warburg: Z" & Z' - 1/sqrt(w)
9.Z’- wZ”
10.Z' - Z"/w
11.Cot(phase)-Sqrt(w)
12.1/wZ” - 1/wZ’
13.Y"/w-Y'/w
法拉第阻抗的理论基础如下 如果施加的电压(A.C振幅)很小(大约5/n mV,其中n是移动电子的数量),那么施加的电压和电流响应之间存在着线性关系。 也就是说,I=E/Rf,其中Rf是法拉第阻抗。
Rf与电子转移率的倒数成正比。 较小的截距是Z'=Ru,较大的截距是Z'=Ru +Rf。 半圆的最大-Z "值所对应的频率等于1/RuCdl。 因此,这个简单的RC电路的三个组成部分可以通过阻抗测量来计算。
奈奎斯特图(Nyquist plot)通常是用来显示最多数据的方法;波德图(Bode plot)比奈奎斯特图有更好的分辨率,如果有一个以上的过程支配反应体系,波德图是有用的。 从阻抗图中可以得到很多信息,但非常复杂,可能难以解析。
例如,在奈奎斯特图中,可能有多个半圆,而且它们往往不在正的象限内。 阻抗测量已被广泛用于电子转移速率的研究,例如在腐蚀和电池研究中使用。 它还被用来测量电子通过电极表面的电化学活性聚合物薄膜的移动速度。
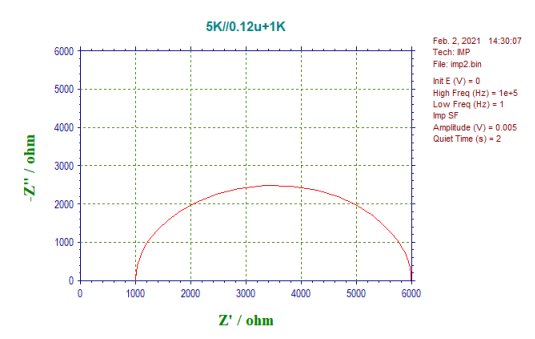
图 17-3. 典型的奈奎斯特图
阻抗时间法(IMPT)
阻抗时间法测量时将基础电位保持在初始电位。在此基础电位上叠加一个正弦波。对电流和电压进行采样,分析实数和虚数的阻抗分量。阻抗被记录为时间的函数。下图显示了作为时间函数外加电位波形。

图18-1阻抗-时间法测量的电位波形
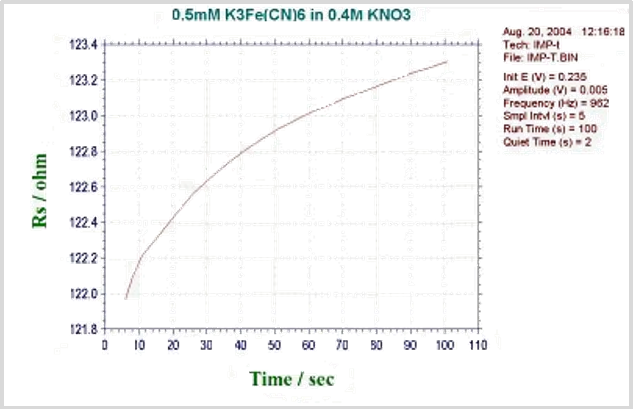
图18-2 典型的阻抗-时间图
可用于绘图的数据类型
1.logZ - t
2.Phase - t
3.Z - t
4.Z' - t
5.Z" - t
6.Log (Z" & Z') - t
7.logY - t
8.Y - t
9.Y' - t
10.Y" - t
11.log(Y' & Y") - t
12.Rs - t
13.Os - t
14.Rp - t
15.cp - t
阻抗电位法(IMPE)
阻抗-电位法是将电位E从初始电位值增加到最终电位值,并将一个连续的正弦波叠加在基础电位E上。对电流和电位进行采样,分析实数和虚数的阻抗分量。
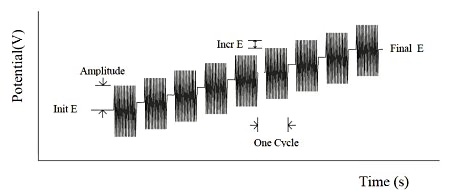
图19-1阻抗-电位法测量的电位波形

图19-2 Mott-schottky图
可用于绘图的数据类型
- LogZ - E
- phase - E
- Z - E
- Z' - E
- Z" - E
- log(Z" & Z') - E
- logY - E
- Y - E
- Y' - E
- Y" - E
- log(Y' & Y") - E
- Rs - E
- Os - E
- Rp - E
- Cp - E
- 1/(Cs*Cs) - E : Mott-schottky
- 1/(Cp*Cp) - E : Mott-schottky
计时电位法 (CP)
计时电位法可以控制通过工作电极的两个电流水平。可以通过对时间或电位的设定来控制电流的极性切换。电位被记录为时间的函数。可以看出,图 46 中的电流波形作为时间函数通过工作电极。
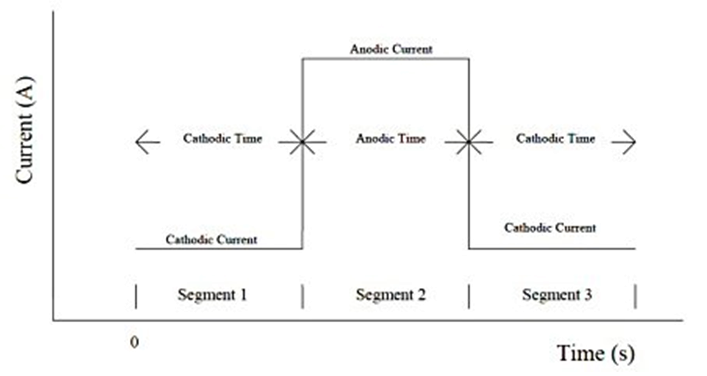
图20-1 计时电位法的电流波形
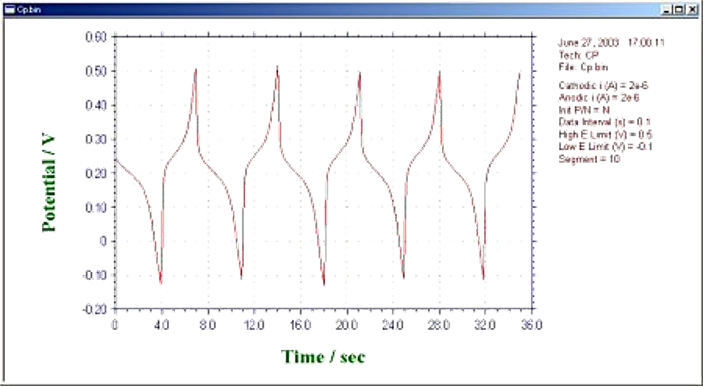
图20-2 电位-时间图
可用于绘图的数据类型
Potential - time
dE/dt - time
dt/dE - time
Potential - charge
计时电位斜坡电流法 (CPCR)
计时电位斜坡电流法是在工作电极上外加斜坡递增的电流。电位被记录为时间函数。下图显示了一个斜坡电流波形作为时间函数通过工作电极。

图21-1 计时电位斜坡电流法的电流波形
扫描步进功能 (SSF)
扫描步进功能可以同时使用 6 个电位扫描和 6 个电位步进。图22-1 显示了电位波形作为时间函数应用。可12段使用,可视为任意波形发生器。由于可以跳过任何段,因此波形控制具有灵活性。电流被记录为时间函数。对于扫描段,可以设置为初始电位和最终电位,也可以通过电位扫描速度来设置。

图22-1 SSF的电位波形

图22-2 全扫描分段图
多电位阶跃法(STEP)& 多电流阶跃法(ISTEP)
1) 多电位阶跃法(STEP)
在多电位阶跃法技术(STEP) 中,可以施加 12 个电位阶跃并且可以进行循环测量。 反应电流被记录为时间的函数。 下图显示了作为时间函数的施加电位波形。
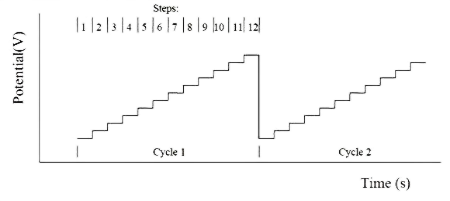
图23-1 STEP法的电位-时间波形
2) 多电流阶跃法(ISTEP)
多电流阶跃法技术 (ISTEP) 最多可施加 12 个电流阶跃,并且可以进行循环测量。 电极电位被记录为时间的函数。 下图显示了作为时间函数的施加电流波形。

图23-2 ISTEP法的电流-时间波形
电位剥离分析(PSA)
电位剥离分析首先应用电位控制沉积步骤。 沉积后,积累在电极表面的每个成分通过施加恒定电流依次溶出释放。 将此时的电位变化记录为时间的函数。 下图显示了沉积阶段的电位和时间设置以及溶出阶段的设置电流。

図24-1 PSAの電位、電流波形
