恒电位仪基础知识连载
- 第一篇:恒电位仪的电路构成及其特点
- 第二篇:双恒电位仪
- 第三篇:正反馈功能
- 第四篇:溶液电阻和iR补偿
- 第五篇:电子转移速率
- 第六篇:氧化还原电位(1)
- 第七篇:氧化还原电位(2)
- 第八篇:氧化还原电位(3)
- 第九篇:氧化还原电位(4)
- 第十篇:氧化还原电位(5)
- 第十一篇:电化学阻抗谱(EIS) - (1)
- 第十二篇: 电化学阻抗谱 (EIS) - (2)
- 第十三篇: 电化学阻抗谱 (EIS) - (3)
- 第十四篇: 电化学阻抗谱 (EIS) - (4)
- 第十五篇: 电化学阻抗谱 (EIS) - (5)
- 第十六篇: 电化学阻抗谱 (EIS) - (6)
- 第十七篇: 电化学阻抗谱 (EIS) - (7)
- 第十八篇: 电化学阻抗谱 (EIS) - (8)
- 第十九篇: 电化学阻抗谱 (EIS) - (9)
- 第二十篇: 电化学阻抗谱 (EIS) - (10)
- 第二十一篇: 电化学阻抗谱 (EIS) - (11)
第一篇:恒电位仪的电路构成及其特点
Professor Noriyuki Watanabe
在以前的技术资料 “对电极’’中,曾经提到过,了解恒电位仪的构成原理有助于理解对电极和工作电极之间的区别。本篇仅就恒电位仪的工作原理及功能进行简要的介绍。在恒电位仪中使用了运算放大器Op amp (operational amplifier)。在此, 我们省略了Op amp (运算放大器)的详细说明, 只是进行概要说明。
运算放大器的特点是,有很大的直流电流增益,高输入阻抗,低输出阻抗及很高放大倍数的放大器。通常可以通过从输出侧反馈到输入侧(例如加法,减法,微分,积分和电压跟随器等的阻抗转换)进行各种运算。因此,只要记住在两个输入端子就没有电流的流入和流出(因为输入阻抗非常大),以及两个输入端子具有相同的电压(两个输入端子之间的电位差为零) 这两点,即可理解大多数电路的配置。
由于运算放大器的这些特性,恒电位仪可以由至少两个运算放大器进行组合形成(图1中的虚线圆的标记代表电化学池,而W,C,Ref分别表示工作电极(Working electrode), 对电极(Counter electrode)和参比电极(Reference electrode)。
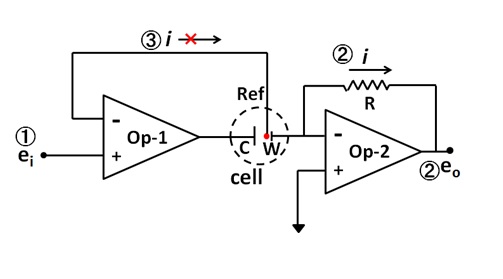
图1. 恒电位仪的基本电路图。
恒电位仪的基本功能可以总结成三个基本点: ① 参照参比电极来控制调节工作电极的电位, ② 测量流过工作电极的电流, ③ 无电流流向参比电极。
首先来看功能①。 从外部施加的电压(设定电位,施加电位)ei 同时也是施加到参比电极上的电压(因为图 1中Op-1的两个输入端子的电位相同)。 另一方面,工作电极的电位为接地电位(图 1 中Op-2的+输入端接地,-输入端为浮置,但由于两个输入端的电位相同,因此电位等同于接地电位。这被称为虚拟接地)。也就是说,参照参比电极工作电极的电位为-ei。通过这种方式来达到功能 ①参照参比电极来控制调节工作电极的电位。
至于功能②,可以发现输出电压与Op-2(图 1)中流过工作电极的电流成正比,这样功能 ②测量流过工作电极的电流即可实现。
参比电极单独连接在Op-1的-输入端。 由于输入端的阻抗极高,因而无电流流过。 也就是说,功能③没有流过参考电极的电流就能达成了。
以上为恒电位仪的三个基本功能。
至此,我们可以发现对电极和工作电极必须连接到恒电位仪内部电路中完全不同的位置。正如在以前的“对电极”技术说明中所提到的,双电极测量体系中难以将对电极和工作电极区分开,而在使用恒电位仪的三电极测量体系中,它们就可被明确地区别开来。
第二篇:双恒电位仪
Professor Noriyuki Watanabe
一个较为典型的应用实例就是旋转环盘电极(RRDE),此外,还可以用作液相色谱检测器中的双工作电极电化学检测器(twin LCEC),甚至有时也可以用于液-液相界面伏安法。 图2是一个由5个运放器组成的双恒电位仪的电路图。与之前相同原理,工作电极1(W1)的电势由运算放大器Op1和Op2(上回的电路仅用一个运算放大器)进行控制,其电势为E1。运算放大器4是一个减法电路,其输出E 1和E2之间的差值信号,同时成了运算放大器5的+输入端(信号差ΔE= E2-E1)。由于+端子和 - 端子的电势相同(如前所述),施加到工作电极2的电势为E2─E1。

图2. 由5个运放器组成的双恒电位仪的电路图
E1为施加到电极1上的电势,E2可以完全独立地选择。 因此,电极2可以被独立地控制。通过这种方式,例如RRDE,可以相对于同一参比电极对盘电极和环电极的电极电势分别进行控制。
最后两点。 一点是电压跟随器。 即就是运算放大器2。 由于除了来自前一级(运算放大器1)的信号之外没有连接到+端子的其他路线,所以几乎没有电流通过。 由于- 端子被连接到参比电极,所以也没有电流通过,因此电流可以通过放大器输出端(连接到反电极C并变成电解电流)流动。 这样有可能在没有电流流动的情况下传导大电流,即执行阻抗转换。 在恒电位仪中经常使用这种方法。
另一点是减法电路和加法电路。 在减法电路中,可能难以清楚地理解输入信号之间没有相互干扰的特性,而对于加法电路来说,只需将加成的变量连接到同一个输入端,因此容易说明它的功效。下一篇将讨论有效使用加法电路进行溶液电阻补偿的正反馈功能。
第三篇:正反馈功能
Professor Noriyuki Watanabe
由于设定电势仅仅是施加在工作电极和参比电极之间的电势,其中还包含了溶液电阻造成的电势下降部分,实际施加到工作电极的电势会由于这一电势降影响而不足。
通常这被称为未补偿溶液电阻,并用Ru表示。
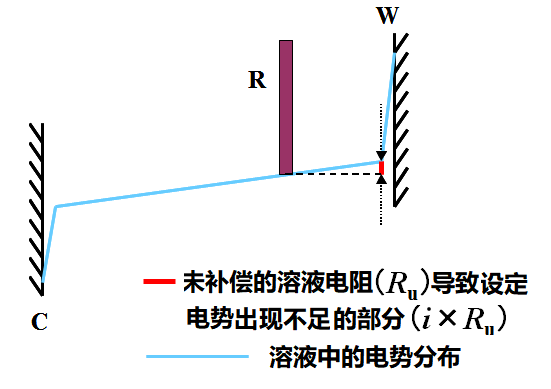
图3.1 未补偿的溶液电阻(Ru)造成施加的电势不足,W,C,R分别表示工作电极,对电极和参比电极。
方法就是进行正反馈处理。 如图3.2所示 正反馈电路可以用三个运算放大器构成。一个加法电路(Op 1)被加入我们前面提到过的基础电路(由两个运算放大器配置)原型中。将电解电流(i)和Ru(即由于未补偿的溶液电阻引起的电位下降)的部分(f)叠加到设定电位(e 1)上,弥补其不足。
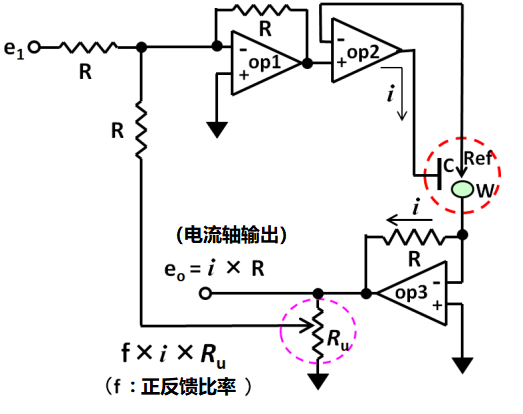
图3-2 用于iR补偿的正反馈电路
使用正反馈功能可以一定程度上改善电化学测量。 切记,正反馈功能本身并不完美。
第四篇:溶液电阻和iR补偿
Professor Noriyuki Watanabe
溶液电阻包含对电极和参比电极之间溶液的电阻(Rs)以及参比电极与工作电极之间溶液的电阻(Ru)(图4-1参考)。
![图4-1. 三电极配置的[[电化学池>http://als-japan.com.cn/1342.html]]的阻抗 图4-1. 三电极配置的[[电化学池>http://als-japan.com.cn/1342.html]]的阻抗](http://als-japan.com.cn/xdata/technical/PS_tab3_1.jpg)
图4-1. 三电极配置的电化学池的阻抗
响应电流可以通过RuCd1的时间常数的指数函数来表示(下式)。
当t = 0时,指数函数为1,所以i(0)=ΔE/ Ru 即,在施加电势瞬间获得的电流值,因为ΔE是设定值并且已知(例如设定为50mV),所以可以得到Ru的值。
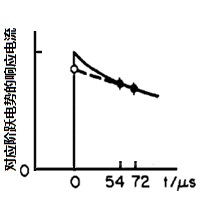
图4-2 微小电势阶跃下的响应电流的经时变化
第五篇:电子转移速度
Professor Noriyuki Watanabe
黑色曲线是电子转移速度为0.1 cm/s(足够快,可认为是可逆的)的模拟CV图形。 两条红色曲线是电子转移速率变慢一个或两个数量级的情况下的模拟CV图形。可以发现,还原峰电势与氧化峰电势之间的峰值电位宽度,随着电子转移速率变慢,渐渐朝着变宽的方向上变化。
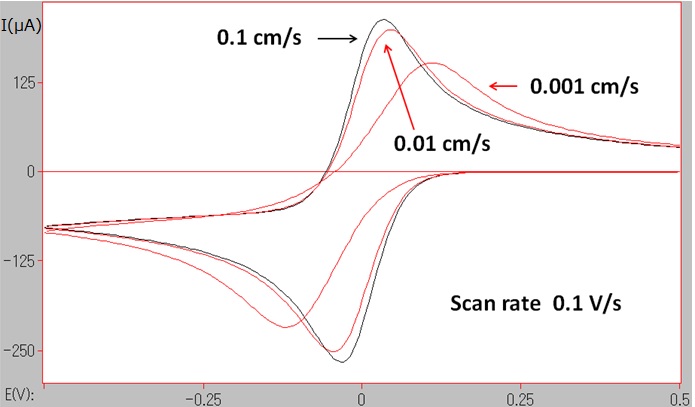 图5-1 不同电子转移速率下的模拟CV图 (Ks = 0.1, 0.01, 0.001 cm/s)
图5-1 不同电子转移速率下的模拟CV图 (Ks = 0.1, 0.01, 0.001 cm/s)
电子转移速度取决于电子转移过程中的活化能的大小,并且还会受到电子转移发生前后的分子的结构变化以及溶剂化作用的影响。研究这样的动力学参数,与研究热力学参数的氧化还原电势氧化还原电位同样,成为电化学测量中的重要目标。
顺便提一下,峰电势宽度(ΔEp)不仅会因电子转移速度的变化而改变,而且未补偿的溶液电阻更是会对其产生很大的影响。 迄今为止,这已经被提及过几次了。
此外,氧化还原电位是用峰电位的的平均值计算得到的,但是由溶液电阻引起氧化峰值和还原峰值之间峰电势的偏移,从而出现不均等的可能性也是应该考虑进去的(虽然是小事)。换句话说,氧化和还原的峰值电流值的绝对值通常不会完全相同的。
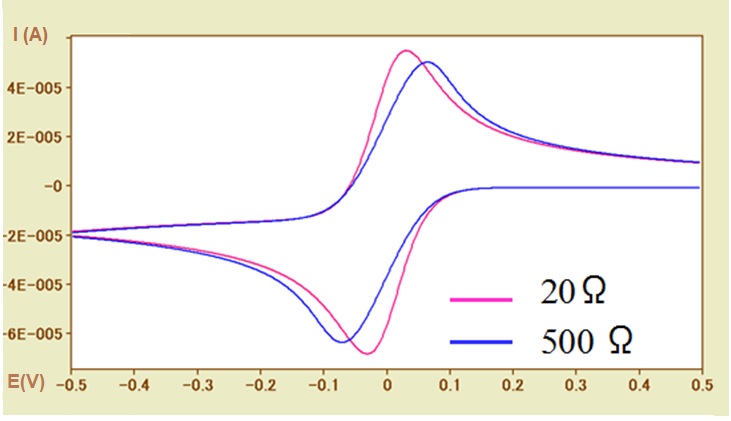 图5-2 不同溶液电阻下的模拟CV图(Ru = 20Ω,500Ω)
图5-2 不同溶液电阻下的模拟CV图(Ru = 20Ω,500Ω)
在图5-2中,氧化峰的基线电流为负值,所以氧化峰值电流的绝对值小于零基线电流的还原峰值电流的绝对值。
由于溶液电阻对电位漂移的影响是在 电流×溶液电阻(电势下降值)时有效,因此电流值也很重要。 可以通过降低电活性物质的浓度,或减小电极反应的面积(极端情况下可以使用微电极)等降低电流值的方法,来判断是否存在溶液电阻的影响。
参考文献
5-1) R. S. Nicholson, Anal. Chem.,37, 1351 (1965)
第六篇:氧化还原电位(1)
Professor Noriyuki Watanabe
物质的外层电子(在此被认为是分子物质)依次从低能级排列进入到较高一级的的能级(也称为轨道)。电子占据的最高的能级被称为最高被占分子轨道(HOMO;Highest Occupied Molecular Orbital),在其上面一级的未被电子占领的轨道被称为最低未占分子轨道(LUMO:),它们是分子参与反应的能级。 因此,HOMO和LUMO也被称为前沿能级轨道。对于电化学反应而言,氧化就是夺取HOMO轨道中的电子,还原是将电子填充进入LUMO轨道中。 由于电子的能级水平是物质固有的特性,所以氧化还原电位也是该物质所有的固定特征值。其正式的名称可以被称为标准氧化还原电位或当量氧化还原电位,但这里表示为氧化还原电位(redox potential其中的redox是还原reduction和氧化oxidation的组合)。
由于分子类的氧化还原电位取决于HOMO - LUMO的位置,在理论上可以通过量子力学计算得到。 但是,定性了解影响氧化还原电位的要素也是非常有用的。 因此,下面将会分几次进行介绍。
HOMO和LUMO决定了氧化还原电位,它们的变动会使氧化还原电位发生变化。 轨道能级的波动主要是受氧化还原中心(发生电子转移的位置)的电子密度,其周围的电荷(正电荷,负电荷,及其大小)的影响,此外还有介质的影响。使用有机金属化合物作为材料时,可以考虑一下如何对其进行表征。 首先,来考虑一下氧化还原中心(部位)的电子密度的增减。 例如,当氧化还原中心的电子密度由于取代基(给电子取代基)的影响而增加时,电子能级上升(变得不稳定),氧化还原电位易于向负方向移位,这让其变得容易被氧化。 另一方面,如果电子密度降低(吸电子取代基),就会发生相反的状况。
举个例子,我们来比较一下乙酰基和甲基分别作为二茂铁的取代基时的情况。 前者的乙酰基是吸电子基团,因而降低了作为氧化还原中心部位的铁离子周围的电子密度,而后者的甲基由于具有电子供给性从而增加了铁离子周围的电子密度。 取代基的有效性几乎与取代基的数量成正比。 比如二茂铁,当其被一个乙酰基取代时,氧化还原电位会朝正方向移动0.25V,当其被两个乙酰基取代时,氧化还原电位会向正方向移动0.47V。 另一方面,被十甲基取代的二茂铁(当所有的氢原子被甲基取代时),其氧化还原电位会向负方向移动500mV。 基本上每个甲基会使氧化还原电位向负方向移动50mV。
第七篇:氧化还原电位(2)
Professor Noriyuki Watanabe
二茂铁的中心铁元素被其他过渡金属元素取代了的化合物称为茂金属,可用作反应中间体或催化剂等用途。二茂铁是在1951年左右,在不同的地方被分别独自发现,在关于其结构的争议发生后不久,即被Wilkinson等人确定了其构造是环戊二烯基团从铁元素的上下两侧将其夹住的夹心结构7-1)。其独特的分子结构和性质引起了人们的注意,二茂铁的结构发现展开了环戊二烯基与过渡金属的众多π配合物的化学,也为今天的有机金属化学的发展掀开了新的帷幕。
那个时候是使用汞电极的极谱法时代,使用高氯酸盐(相对于SCE为0.31V)作为支持盐的水-醇混合溶剂体系中,用滴汞电极测量氧化还原电位7-2)。 其欺骗性在于它可以在汞电极本身的阳极溶解发生的电势范围内很好地进行测量。
在1959年实现了纯有机溶剂体系中的氧化还原电位的精确测量7-3)。这是堪萨斯大学的三名研究生在复活节的短暂休假期间内完成的研究。以Ted Kuwana为主,另外的两人是分别属于有机化学系的不同实验室的研究生。他们2人是负责二茂铁和几种二茂铁衍生物,二茂钌和二茂锇化合物的合成和提纯。 那时,循环伏安法不像现在那么普遍,Kuwana使用了计时电位法(CP),通过施加恒定电流记录工作电极的电势随时间的变化。尽管现在计时电位法(CP)的使用机会较少,但因为无需对电极电位进行反馈控制,如果能够准确记录电极电位的话,那么这是一种相当简单的测量方法。氧化还原电位可以从通过转移时间来求得。
最初,Kuwana使用了汞电极,但因其本底电流太大,随后铂电极就被用作替代工作电极。要知道当时他的导师就是作为固体电极先驱者而出名的拉尔夫·亚当斯(Ralph Adams),因此使用铂金电极来代替汞工作电极是很自然的事情。
有趣的是,Kuwana的论文的作者署名栏中并没有导师的名字记载。对于包括这个轶事在内的详细情况可以通过Bill Geiger的评论7-4)来了解。 最近,我 (Watanabe) 询问了Kuwana,然后收到了他的电子邮件回复。其中一部分的内容摘录为 “We did most of the work over Easter holiday. The faculty graciously let us publish without their names on the papers. Generous and unusual, needless to say.” (“我们在复活节假期做了大部分工作。老师们慷慨地让我们在论文中不用写他们的名字。无须多言,他们是如此的慷慨和不同寻常。”)。Kuwana的论文揭示了二茂铁的重要性在于其氧化还原电位可以根据取代基进行控制,从这一点上看这是一篇非常令人感兴趣的论文。
参考文献
7-1) Wilkinson,G., J.Am.Chem.Soc. 74, 6146, & 6148, (1952).
7-2) Page,J.A., Wilkinson,G. J.Am.Chem.Soc., 74,6149,(1952).
7-3) Kuwana,T.,Bublitz,D.E., Hoh,G. J.Am.Chem.Soc., 82, 5811, (1960).
7-4) Geiger W.E., Organometallics 26, 5738 (2007).
第八篇:氧化还原电位(3)
Professor Noriyuki Watanabe
在许多有机过渡金属化合物中,当有Π电子受体的羰基(CO)配位时,中心金属离子的氧化电位会朝正方向发生较大的偏移。这是由于从中心金属的对称轨道到配体的反键Π轨道的逆向电子供给(back donation),导致中心金属的电子密度降低。
金属羰基化合物通常具有高电位并且随羰基的数量变大而成比例地增加(图8-1)。 相反,当从羰基这边观察时,因为反键轨道上电子的增加,C = O键结合力减弱,导致CO键伸缩振动频率的降低。
因此,可以通过红外光谱估算逆向电子供给的程度,通常把氧化还原电位测量和IR测量结合使用。
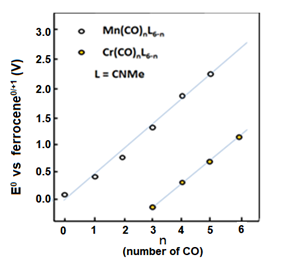
图8-1 用羰基代替锰和铬化合物中的异氰酸甲酯
时的氧化还原电位的变化。
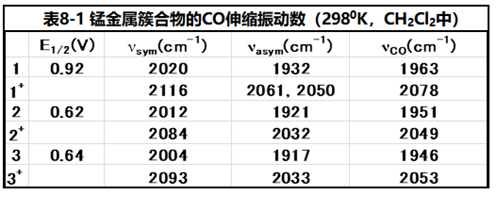
以下为化合物金属锰的簇合物(参考文献8-1)的实例。
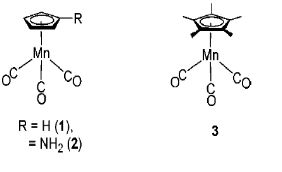
图8-2 过渡金属锰的簇合物。
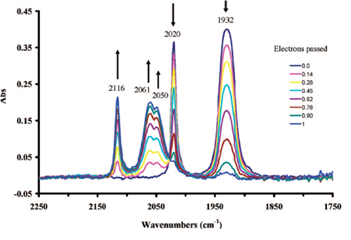
图8-3 化合物1在整体电解氧化过程中的红外光谱变化。
整体电解氧化过程中羰基区域的IR光谱如图8-3所示。
随着电解氧化的进行,属于化合物1的在低波数侧的CO伸缩振动的两个峰发生衰减,在高波数侧出现了3个属于1+ 的三个峰,并且随着电解的进行吸收强度逐渐增加。电解氧化会减少锰周围的电子,使得逆向电子供给作用减弱。 因此Mn - CO键减弱,与此相反CO键结合增强。环戊烯基环上有氨基或甲基取代的化合物2和3(图8-2)的氧化还原电位与化合物1相比,处在其负方向的位置。 这是由于取代基的供电子特性,增加了从中心金属对配体的逆向电子供给,导致了CO伸缩振动的红外光谱中的波数出现了向低波数方向的位移(参见下表)。
8-1) W.E. Geiger et al., J. Am. Chem. Soc., 130, 9859 (2008)
第九篇:氧化还原电位 (4)
Professor Noriyuki Watanabe
一般而言过渡金属原子外层价电子数为18电子(价键理论VBT,18电子规则)。 在此让我们考虑6配位的八面体配合物。 在配体产生的晶体场中,中心金属的5个简并d轨道,被分裂为低能级的t2g轨道(三重简并轨道:dxy ,dxz ,dyz,π型)和高能级的eg轨道(二重简并轨道: dx2-y2, dz2,σ型)(两组简并轨道的能极差为晶体场分裂能Δ)。
d轨道中电子的排列状态取决于晶体场分裂能Δ的大小,以及电子成对时产生的不稳定化能(P)两者的综合作用。如果不稳定化电子成对能P大于晶体场分裂能Δ,为避免电子成对,d电子会优先依次分别填入三个t2g轨道,随后再依次填入2个eg轨道中,此时各个轨道上的多数电子呈平行自旋(高自旋型)的排列状态。 相反,如果晶体场分裂能Δ大于电子成对能P,即使付出克服电子成对能的代价,也可以让6个电子成对排列在更稳定的t2g轨道(低自旋型)上。
当氧化还原中心是金属(HOMO和LUMO能级来自金属)原子或离子时,氧化还原电位会因为HOMO或LUMO能级为eg轨道还是t2g轨道而出现很大的差异。 如果为t2g轨道,氧化还原电位会倾向正电位。由于晶体场论源于配体电荷形成的静电相互作用,因此只能认为是σ型分子键的相互作用。
结合π键相互作用的配体场理论和分子轨道理论更为实用。金属原子(离子)的3d,4s和4p轨道(以第一周期过渡金属系为例)和具有相同对称性的配体轨道(σ和π轨道)彼此产生相互作用。通常,金属的d-轨道能级高于配体的σ-轨道能级,并且低于配体的空的π-轨道(半键合轨道)能级。
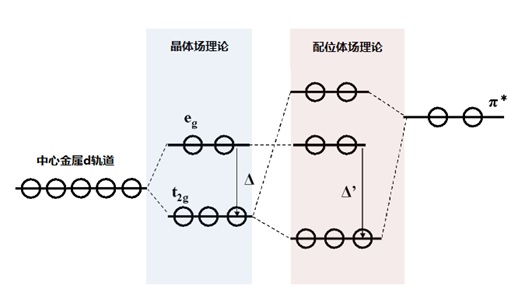
图9-1 dπ(t2g)-π*相互作用图。
NH3 < NCR < PBu3 < PMe3< P(OMe)3< PPh3 < P(OPh)3< PCl3< PF3< CNR < CO
如果t2g轨道处于HOMO-LUMO能级,则由于其趋于稳定(向下)化方向,氧化还原电位就会向正向移动。基于这一原因,与羰基或异氰酸酯配位的金属化合物的氧化还原电势为正电势。另一方面,由于氨基具有低的π接受性并且不降低t2g轨道能级,因此氨基化合物的氧化还原电势倾向于显示为负电势。
在上一篇中所述,因为对羰基的反向供电子效应从而降低了金属周围的电子密度,氧化还原电位发生了正向移动,从而使其难以被氧化,其原因便可用上述配位体场论进行解释说明。
第十篇:氧化还原电位 (5)
Professor Noriyuki Watanabe
本系列第三篇文章中提到的Mn[(CO)6-n(CNR)n]+,10-1). 是通过分子轨道计算,HOMO能量与有机金属化合物的氧化还原电势之间线性关系的典型示例1。CNR是烷基或烯丙基异氰酸酯。 羰基是σ供体和强π受体。 异氰酸烷基酯也σ供体和π受体,但其π受体性能不如羰基强。
如前一篇文章所述,当结合CO基时,金属的d轨道(也是π型)的t2g电子与CO的π ∗轨道(CO的半键合轨道)强烈相互作用,并且金属与羰基发生逆向供电子。前篇所述t2g轨道由于与π ∗轨道的相互作用而被向下推动,因此氧化还原电势向正方向倾斜。
由于电子被提供给配体,因此金属周围的电子密度降低。导致金属中心不易被氧化,因此其氧化还原电势向正方向移动。亦或金属周围的电子密度降低,有效核电荷增加。结果HOMO能级降低(稳定)。 HOMO能级的降低导致氧化还原电势的正向移动。在任何情况下随着结合的CO基团的数量增加,氧化还原电势向正方向上移动。相反,当CO的数量减少时(当n增加时),氧化还原电势向负方向移动。
Pletcher等人10-1)给出了以下关系式 。
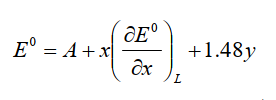

图10-1受体数目和氧化还原电位
A是由所使用的介质(溶剂和支持电解质),参比电极等决定的常数,x是羰基取代基配体数,y是配合物的电荷。 与y前的相关系数1.48是通过对具有相同羰基数和等电子结构的羰基配合物的测量值求平均而获得的值(参见下表)。 表示1.48V,电荷增加1时的正向移位。 该值具有普遍的参考作用。
在周期表中,在相邻原子具有相似原子的氧化还原体系中,原子序数较小的金属通常倾向于在负电势下显示出氧化还原反应。 对于六羰基的一系列V,Cr和Mn等电子配合物,这种趋势是正确的。[ V-(CO)6; -0.35V, Cr(CO)6 ; +1.12V, Mn+(CO)6 ; +2.62V ]
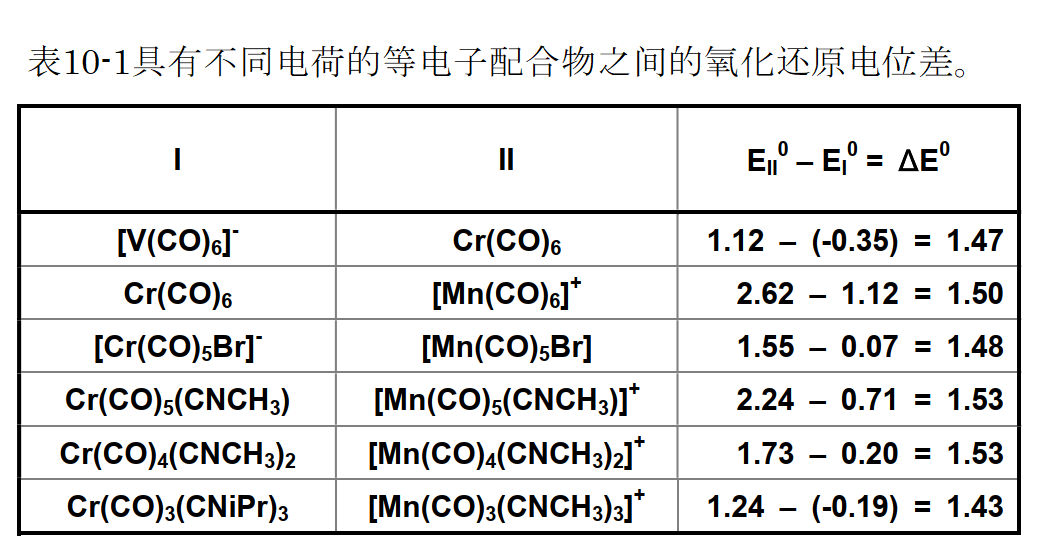
参考文献:
10-1) Pickett, Pletcher, J. Organometal. Chem., 102, 327 (1975)
第十一篇: 电化学阻抗谱 (EIS) - (1)
Professor Noriyuki Watanabe
为什么它们会经常出现? 一般来说电化学研究中的大部分内容涉及到异相介质体系,即电极-溶液界面上的电荷移动现象。在异相介质界面上,就会形成具有正负电荷对的双电层。 换句话说,也就是电容。而且如果要使电荷移动,则需要进行激活。 这就对应于电阻。 电容和电阻这两者往往是同时发生的,而不是前后逐渐出现。 有非常多的状态和现象,可以由电阻和电容的并联电路(同时进行)进行替代。
在右图中插入了等效电路以帮助理解(在分析EIS时,等效电路是用电子电路元素代替现象、过程等直观解释现象、过程等的辅助手段)。 它是由电容C和电阻R的并联回路及与之串联的电阻Rs组成的等效电路。
如果我们假设C是电极界面双电层的电容,则并联的电阻R可以认为是电极与电活性物质之间发生的电荷传递电阻。 电荷传递速度越快,电阻越小。电荷传递速度取决于各种因素,如活性材料的类型和浓度、电极的电势和供电方式等。
串联的电阻Rs代表什么?其相当于未补偿的溶液电阻,即工作电极和参比电极之间的存在的溶液电阻,即使是电位器也无法补偿。 换句话说,它是电化学系统中常见的等效电路。 这就是一直以来被称为的 "Randles电路"。
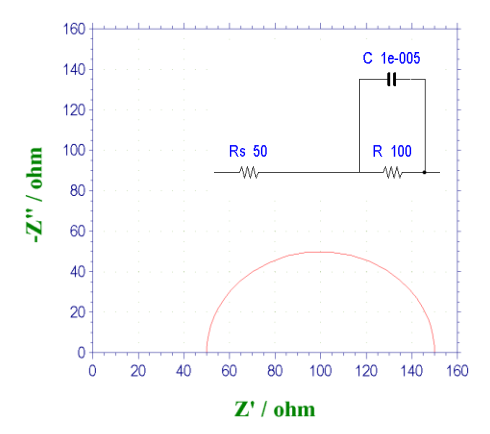
图11-1. Nyquist图例
接下来我们解释一下Randles图的用处。 以频率为参数在横轴和纵轴上绘制将小幅度可变频率AC电势施加到工作电极时的阻抗响应的实部和虚部。 在高频下,由于电容C引起的阻抗接近零,因此可以将界面阻抗视为零(电荷转移电阻不起作用,因为它相当于被短路)。然后只剩下溶液电阻。 即在半圆和实轴(X轴)的交点中,更接近原点的那一个值对应于溶液电阻值 Rs 。
另一方面,在低频下,源自电容的阻抗变得非常大,结果,仅电荷转移电阻分量变得可见。 溶液电阻Rs和电荷转移电阻R之和对应于远离原点和实轴的半圆的交点(频率为零)。半圆顶点处的频率fmax (在Nyquist图中,频率是一个隐藏的参数,可以从Bode图中得到)代入关系式 fmax = 1 / (2πRC).来计算电容值。 这样,您可以知道要查找的三个数值。
频率fmax的倒数是时间,并且可以获得诸如过程的弛豫时间,持续时间和寿命之类的信息。 通常,在Nyquist图中,高频对应于一个更靠近原点的频率,而一个远离原点的频率对应于零频率。 以上是在Nyquist图的典型用法。
第十二篇: 电化学阻抗谱 (EIS) - (2)
Professor Noriyuki Watanabe
阻抗测量的基本点是测量响应交流电流的振幅和相位差(所以数据的表示方式基本上是二维的)。 这时,交流电压的频率会逐步发生变化。 通常的做法是,以10倍于预设次数的频率范围晃动约5个点。 因此,低频测量比高频测量花费更多的时间。 因为一个点所需的时间取决于频率,所以测量目标必须处于稳定状态。阻抗测量基本用数学方程式表示如下。
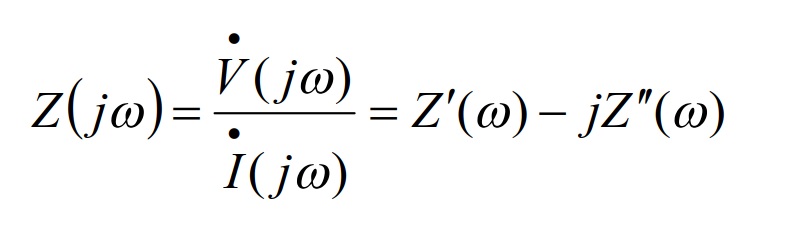
有两种表示阻抗数据的典型方法。就是上一篇中说明的奈奎斯特图(Nyquist plot),和另一个伯德图(Bode Plot)。在奈奎斯特图中,阻抗的实部和虚部分别绘制在实轴和虚轴上。此时,频率被绘制为一个变量,但是由于它是一个隐藏变量,因此很难清楚地看到它,这是奈奎斯特图的一个缺点。但是,如果系统中包含多个基本过程,并且它们的时间常数彼此广泛分离,则基本过程的数量可以看作是一些特征半圆组合而成的图。 直观易懂,方便获取整体视图。
另一方面,在伯德图中,横轴是频率的对数,纵轴是阻抗和相位差的绝对值的对数。这种图形表示的特点是很容易看到阻抗的绝对值和相位差发生变化的频率范围。 由于这两种表示图形都有其自身的特性和优点,因此很容易理解将Nyquist和Bode图一起显示。 分析EIS时,通常的做法是用电子电路中使用的元件(电阻,电容,线圈(感应)等)代替各种电化学基本过程。 在电化学基本过程中,仅电子电路元件是不够的,还添加了与扩散现象相对应的Warburg阻抗(包括自由扩散和有限扩散)和具有扩展容量的CPE(Constant Phase Element)。 将在下一篇详细介绍这些元件。
第十三篇: 电化学阻抗谱 (EIS) - (3)
Professor Noriyuki Watanabe
让我们看一下电路元件的奈奎斯特图。 首先考虑仅由电容组成的对象(图13-1)。就是电容用作电路元件。对于直流其不能通过电容,所以没有电流流动。 这对应于电极表面处于没有氧化还原发生的电位区域中的情况。即,它对应于极化电位区域中的电极。其表示符号代表导线在中间被切断,这意味着通常直流电流不能通过,这真的很容易理解。符号象征性地代表了实体的特征。
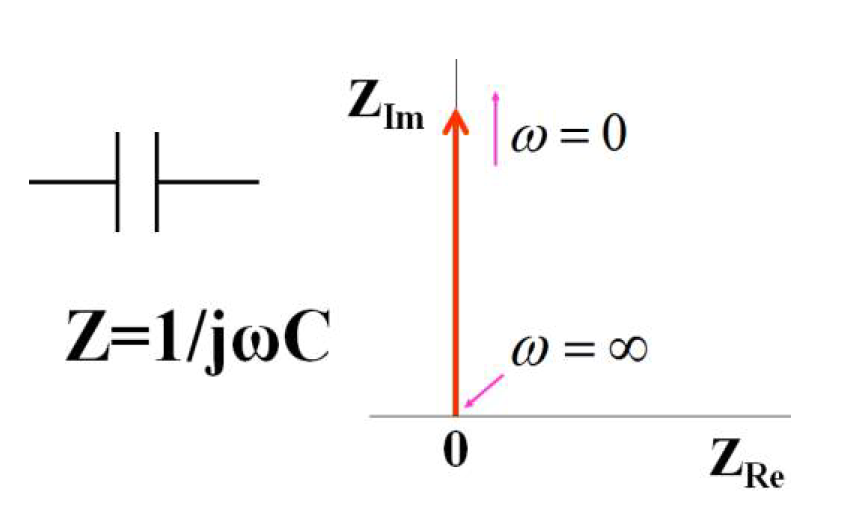
图13-1 电容符号,表达式,奈奎斯特图
用数学公式表示时,Z = 1 ⁄ (ωC),而在奈奎斯特图中,其与虚轴重合。 当频率接近∞(无限大)时,阻抗接近零(在奈奎斯特图中的原点)。 如果交流频率很高,则交流电流将很容易通过电容器。 相反,若频率为零,即直流电流就不能流过。 换句话说,此时阻抗变得无限大,因此它变成一条直线,该直线发散到无穷大并从原点垂直上升。 这是容量的奈奎斯特曲线(图中的红色箭头→与虚轴重合)。
现在,如果将电容与电阻连接时出现什么情况?有两种连接方式。电阻与电容串联或并联。电阻的意思是,当电子或离子移动时阻碍它们移动的作用力。 它是伴随电荷传递一起出现的元素。 在这种情况下,电压和电流之间没有相位差。
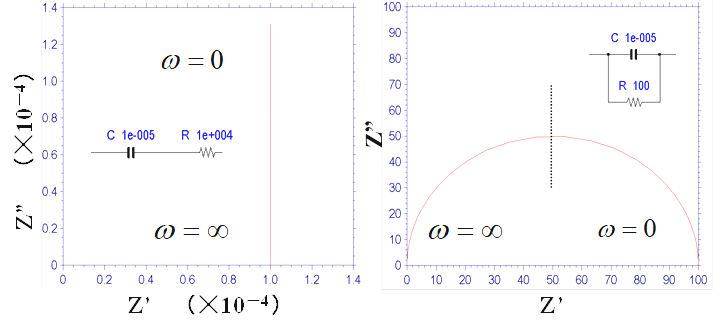
图13-2 电容和电阻串联(左图)和并联(右图)时的电路的奈奎斯特图
这种并联连接的电路可以看作一个基本的过程,并且电阻值×电容值=时间常数。 对应于半圆的顶点的频率的倒数等于时间常数。因为知道顶点频率会给出有关基本过程时间的信息,非常重要必须强调的是这会经常使用。图13-2 中的左图对应于从原点开始平移了电阻值的极化电极,右图对应于溶液电阻为零时的电子传递电极,但实际上溶液电阻不可能为零。 通常可以看到从原点平行移动了溶液电阻值的一个半圆(第十一篇 图11-1. Nyquist图例)。 对于左图而言,一般来说倾斜的直线或曲线较为常见,而不是垂直上升的直线。
第十四篇: 电化学阻抗谱 (EIS) - (4)
Professor Noriyuki Watanabe
扩散在电化学反应中起重要作用。 长期以来,称为Warburg阻抗(Zw)的元素已被用来表示涉及扩散的过程,并由复式方程(1)表示。
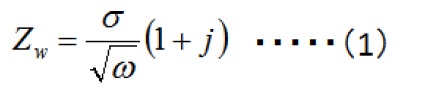
上式中的系数σ:
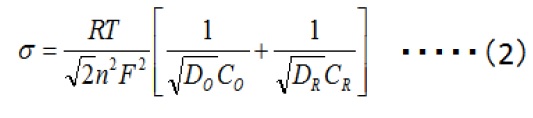
如式(2)所示,系数σ包括活性物质的浓度(CO,CR),扩散系数(DO,DR)和转移的电子数n,以及角频率ω(可用频率f代替)。 由此决定了阻抗的大小。随着浓度、扩散系数和频率的增加,阻抗减小。当浓度和扩散系数固定时,该过程在低频下起作用。
图14-1 显示了Warburg阻抗的奈奎斯特图。 从等式(1)可以看出,实数分量和虚数分量相等,因此相位始终恒定为45°,并且直线与实轴成45°角。 通常大部分过程出现在低频区域。
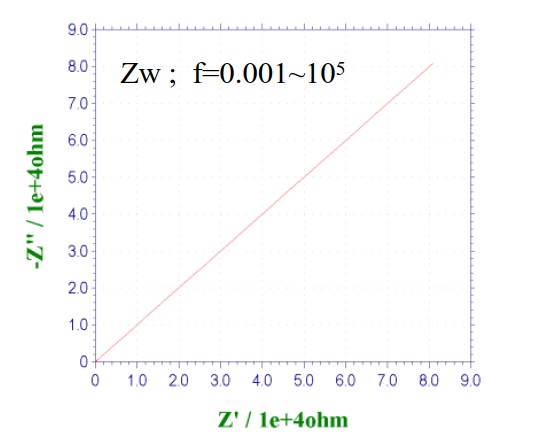
图14-1Warburg阻抗的奈奎斯特图

图14-2 Randles 电路
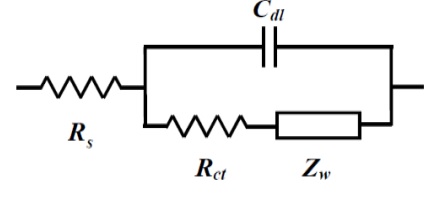
图14-3 含Zw的Randles 电路
如上一篇所示,从原点开始的半圆形Nyquist图是由CR并联电路产生的。 当溶液电阻与之串联时,溶液电阻可以从半圆从原点移动的部分来得到。
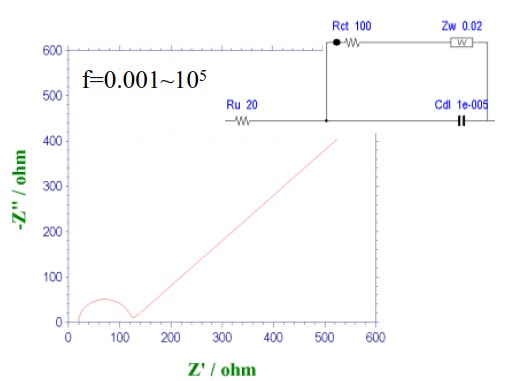
图14-4 含Zw的Randles 电路的奈奎斯特图
相反,在像二茂铁这样具有极快电子传递速度的体系中,则只能看到45°的直线而看不到半圆。
第十五篇: 电化学阻抗谱 (EIS) - (5)
Professor Noriyuki Watanabe
本篇来谈谈称为CPE(Constant Phase Element恒定相位元件)的等效电路元件。 在实际测量的奈奎斯特图中的半圆通常表现为不规则的 (变形的) 半圆,而不是理想的半圆形状。
这种现象是由于电极的不均匀性(电极的几何形状等而使得电位及电流密度的不均匀性,电极表面的凹凸,吸附和被覆盖程度等的各种表面的物理性质,化学性质上的非均匀性分布)而产生的。 下式表示的CPE阻抗通常用来描述这种现象。
CPE阻抗由两个参数Y和n来表征,n取值范围是从-1— 0 — 1。 如果n = 1,则为纯电容,如果n = 0,则为纯电阻;如果n = -1,则为电感。 Y对应于导纳(阻抗的倒数)。 若时单独使用CPE,其奈奎斯特图是一条相对于实轴具有一定角度的直线,如图15-1所示。一般来说CPE不会单独使用,而是经常在和电阻并联的电路中使用,如下面的图15-2和图15-3所示,在奈奎斯特图中为一个变形压扁的半圆形。 因此,它通常被解释为变形的电容。如果要想得到与实验结果匹配的模拟效果时,最好使用CPE,但必须认识到这并不意味着其实质已被解释清楚。
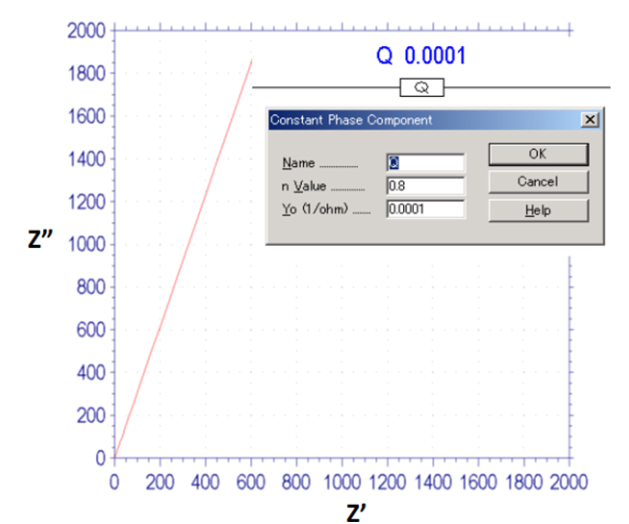
图15-1 CPE的奈奎斯特图,n=0.8时 。
如果只有双电层容量,而没有并联的电极活性材料,或者设定电位与活性材料的氧化还原电位偏差太大,以至于没有电极反应发生(即Rct=∞),则Nyquist图应该显示一条垂直于实轴上升的直线。 但是,在实际的电化学体系中,特别是在多孔电极中,很少见到垂直于实际轴线上升的线,多数可看到的是有一定斜率的直线。可以看到这种情况对应于图15-1。 包含上述情况,如果CPE和电阻并联时,则奈奎斯特图会显示为变形压扁的圆弧。当n = 0.8时,曲线形状如图15-2所示。 当n的值进一步减小时,压扁变形会更加严重(图15-3)。

图15-2 CPE和电阻并联电路的奈奎斯特图,n=0.8 时。

图15-3 CPE和电阻并联电路的奈奎斯特图,n=0.6 时。
第十六篇 电化学阻抗谱(EIS)-(6)
Professor Noriyuki Watanabe
半圆的直径与每个并联电路的电阻值R匹配。 电阻为100Ω的过程对应于最大的圆弧。时间常数是10-2秒,它出现在最低频率侧,反映了最长的基本过程(正如之前提到的,在奈奎斯特图中越接近原点处的频率越高,越远离原点处的频率越低)。
在图16-1 中,5×10-6秒的基本过程出现在最高频率侧,反映了最短的时间常数,并对应于具有最小并联电阻的过程。中间的圆弧与时间常数为10-4秒的基本过程相对应。 使用等式fmax = 1 /2ΠCR从半圆的峰值频率(fmax)和电阻值R可获得电容C的值。
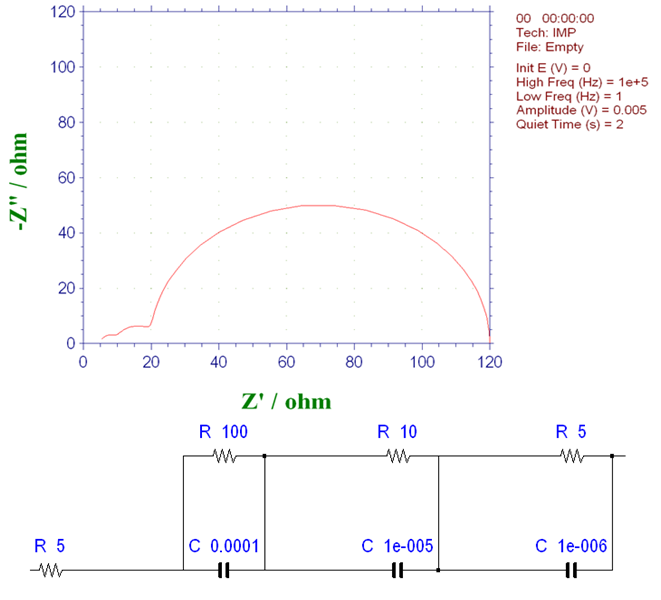
图16-1 含三个连续发生的基本过程体系的奈奎斯特图 (1)
在寻找这些等效电路的过程中,必须考虑等效电路是否适当地对应于实际的化学和物理现象。从这个意义上讲,电阻,电容和Warburg阻抗很容易考虑。
例如,电阻反映了介质本身的电阻,界面处的电荷传递速率以及溶液,薄膜和各种其他介质中离子传输速率的大小。如果电极上的电子传递速率较慢,则对应于较大电阻。 由于极性界面的形成,电荷的充电/放电等形成了电容。
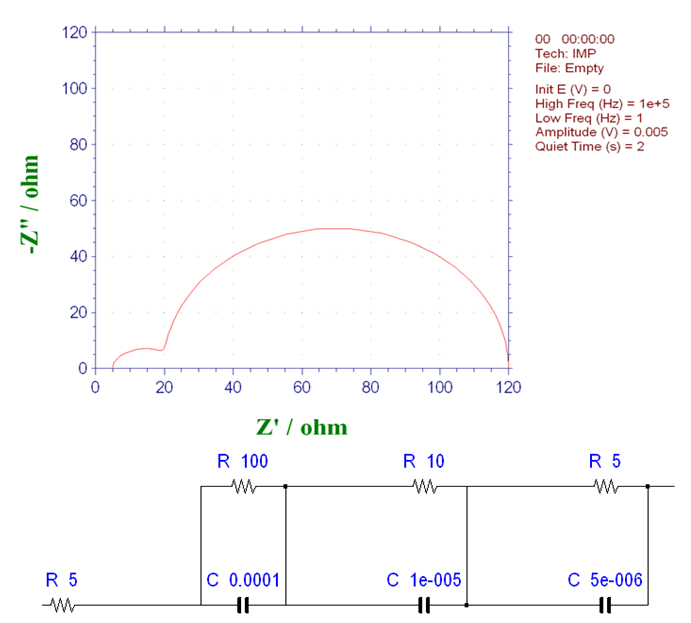
图16-2 含三个连续发生的基本过程体系的奈奎斯特图 (2)
此外,在各种涉及扩散的现象中都会出现沃伯格(Warburg)一词。 幸好这些现象的时间常数具有经验累积或可以粗略地估算出来。 另一方面,对于CPE,我们可以通过模拟构建一个与测量结果相适应的模型,并得到结果。 但在数学上,根据n的选择,其模型可以是电容、电阻或电感,因此必须认识到仅从这些是很难描述其化学现象或物理现象。
第十七篇 电化学阻抗谱(EIS)-(7)
Professor Noriyuki Watanabe
第一种称为Nernst扩散模型(Nernst diffusion, ND)。 当运动受到限制时,可称为有限扩散(finite diffusion, FD)模型。即使扩散层的厚度是有限的,但移动不受限制,旋转电极和质子交换膜型燃料电池(PEMFC)支持ND扩散。 ND的阻抗由下式给出。
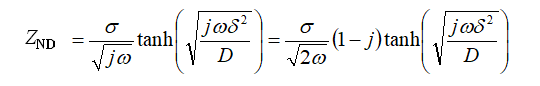
式17-1
此公式的模拟曲线图例如图17-1所示。(a)(b)(c)中的 Rs = 0,Rct = 8,Cdl = 10-4,D = 10-4为相同值时,可以看出当改变浓度C和膜厚度δ的参数时在奈奎斯特图中的曲线形状的变化。

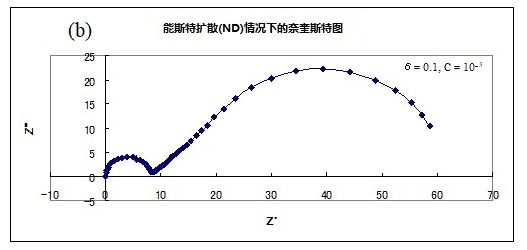
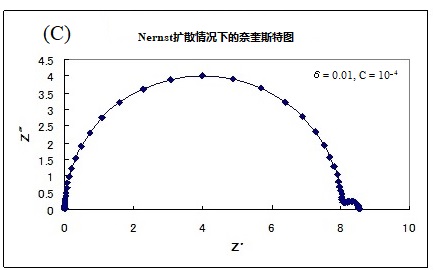
(a) δ= 0.1, C = 10-4 (b)δ= 0.1, C = 10-5 ( c) δ= 0.01, C =10-4
各图中的左侧高频侧的半圆是由于电极上的电子转移和界面双层电容的并联回路,大小不变(注意,横轴的大小不同。 它们是具有相同电阻值和相同直径的半圆形)。可以发现斜率为45°的直线的长度和随后在低频侧的弧线的大小会因膜厚度和浓度而改变。虽然只有一个电极过程,但明显出现了两条弧线。 在半无限扩散中低频侧原本是一条直线,却形成了另一个半圆。 虽然由于扩散造成的半圆比由于电极过程造成的半圆大,但它的特点也是,在低频范围内,与实轴成45度角的直线部分仍在半圆的高频侧,这就是在PEMFC和RRDE阻抗测量中经常看到的奈奎斯特图。
第十八篇 电化学阻抗谱(EIS)-(8)
Professor Noriyuki Watanabe
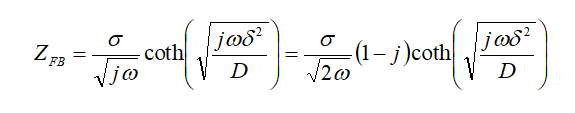
式18-1
图1显示了该等效电路的模拟结果。 电荷转移电阻(Rct)、双层容量(Cdl),有限膜厚度δ,扩散系数和浓度(如图所示),溶液电阻为零。当然,溶液电阻是存在的,但它只移动实轴上的位置,所以省略了。电荷转移过程的半圆之后,经过一定长度的45度梯度的直线,在低频带垂直于实轴上升。当有限膜厚度δ减小时,45度的直线就会变短。
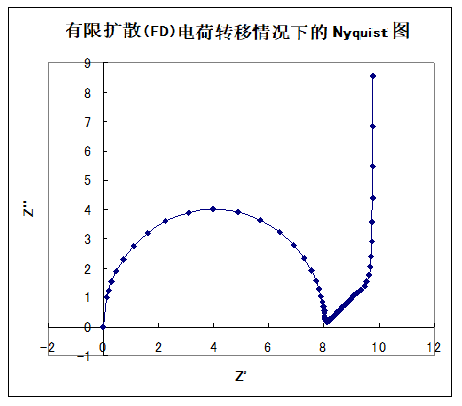
图18-1.有限扩散电荷转移情况下的奈奎斯特图
Rct(·)=8,Cdl(F/cm2)=0.0001,δ(cm)=0.1,
D=0.0001 cm2/s,C(mol/cm3)= 0.0001

图18- 2 碳球电极(30µm直径)示意图
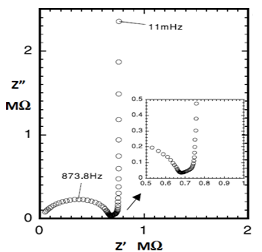 图18-3 锂离子嵌入微碳球电极的奈奎斯特图
图18-3 锂离子嵌入微碳球电极的奈奎斯特图
[18-1] Uchida et al.,Electrochimica Acta 47,885(2001)
[18-2]J.Newman et al.,J.Electrochem.Soc.147 293 0(2000)
[18-3] M.D.Levi et al.,J.Phys.Chem.B 108,11693(2004)
第十九篇 电化学阻抗谱(EIS)-(9)
Professor Noriyuki Watanabe
上侧线上的rt是源于电子在氧化钛粒子中的移动速度的电阻分量的微分贡献,下侧线是溶液侧的电阻分量的微分贡献,因为其很小,可以忽略不计。 连接上下两条线之间的并联回路,相当于在纳米粒子/溶液界面的电子的再结合反应速度的电阻成分的微分的贡献rk,与界面双层电容和化学电容(对应于注入二氧化钛颗粒中的电子密度的变化)的组合电容的微分贡献Cm所组成。 该模型的阻抗由式(19-1)给出。
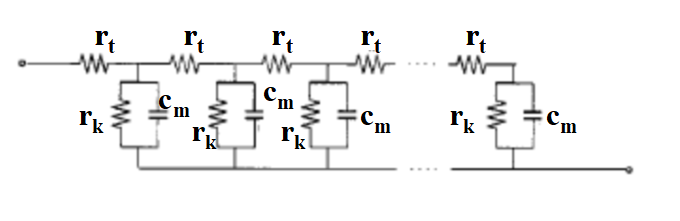
图19-1 TiO2阳极传输线模型图
 式(19-1)
式(19-1)
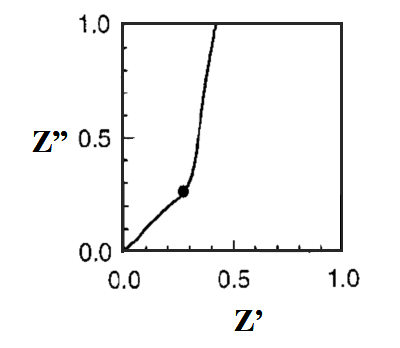
图19-2 TML模型,如果Rt<<Rct
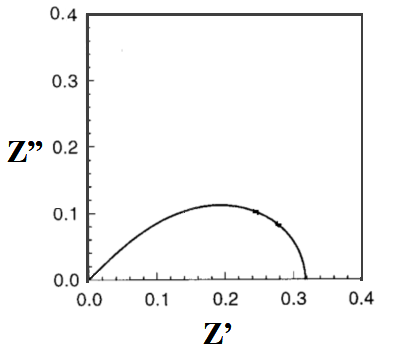
图19-3 Rt>>Rct的情况
当TiO2薄膜电极的厚度为L时,Rt=rtL、Rct=rk/L、Cm=cmL, ωk=1/CmRct, ωd=1/CmRt的关系。 Rt<<Rct时,Z=(Rt/3)+[Rct/{1 + (iω/ωk)}]成立,奈奎斯特图如图19-2所示。另一方面,Rt>>Rct则Z=RtRct/{1+(iω/ωk)}]1/2如图19-3所示。 作为DSSC,像图19-2那样,Rct很大(即注入的电子的再结合较少)的情况更为可取。 图2是高频率部分的放大表示。
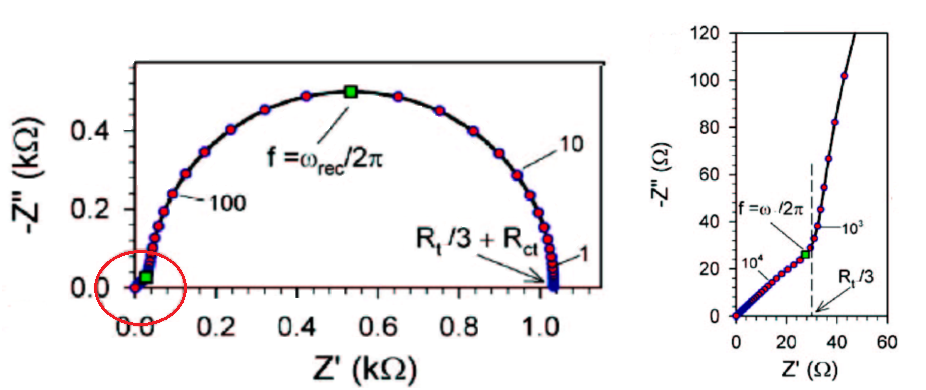
图19-4 Rtct>>Rt,氧化钛阳极的奈奎斯特图
Rt是介孔氧化钛电极中的电子移动有关的电阻,最好是尽可能小。Rct(或Rrec)是氧化钛电极中电子的再结合反应(主要是用于电解液中的I3-还原的消耗)的电阻,再结合反应越慢,Rct就会变大,对于DSSC来说是理想的。
Cm是注入到TiO2中的电子数量的反映,因此期望其能越大越好。RctCm是低频率区域半圆的时间常数,该值大说明半圆尽可能地出现在低频,且该半圆的直径大。 电阻值越大,半圆越大越好,这可能会被认为是奇怪的,但这是因为电子的再结合反应速度越慢,损耗越小,DSSC能够有效地发挥作用。 这是Bisquert等人的小组开发和发展的方法1)该方法也适用于最近突然引起关注的钙钛矿型SC的分析。
参考文献
[19-1] J.Bisquert et al.,J.Am.Chem.Soc.,130,11312,(2008)
第二十篇 电化学阻抗谱(EIS)-(10)
Professor Noriyuki Watanabe
电化学测量基本上是3电极法,但由于研究对象结构上的限制,很多情况下不得不采用省略参比电极的2电极法。 例如,染料敏化太阳能电池(DSSC)、燃料电池、锂离子电池等都是如此。双电极法的EIS测量反映的是工作电极和对电极的总和情况,不能将工作电极和对电极的测量情况进行区分。在这种测量方式下想要单独了解工作电极或对电极的信息是很困难的。在DSSC中,纳米多孔氧化钛膜用作阳极,Pt电极用作阴极。 除了反映每个电极的性能的EIS信息之外,还添加了溶液组分中离子的扩散信息等的贡献。在实际的DSSC中几乎不可能将参比电极插入阳极和阴极之间的问题,因此难以除去阴极,仅测量阳极的阻抗。
本篇,将介绍一个设法加入参比电极的DSSC测量池的例子1)。由于要加入一个参比电极,其在结构上与实际的DSSC稍有差别,但是对于区分阴极和阳极各自的贡献是很有用的。 图20-1是测量池的示意图。将参比电极(直径为0.2 mm的铂丝,表面覆盖黑铂)插入阳极和阴极之间(间隔为1.5 mm)。
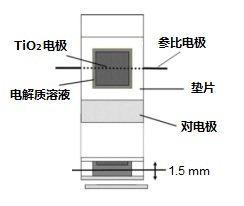
图20-1 三电极DSSC的示意图
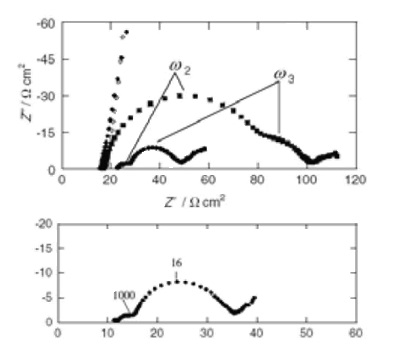
图20-2 总阻抗(上)与阳极阻抗(下)对比
图20-2是利用该测量池得到的奈奎斯特图。上方图是改变阴极(对极)Pt量的4种电池的总阻抗的测量结构。需要测量总阻抗时,只需使用阳极和阴极进行测量,而不使用参比电极。Pt含量少的两个测量池,由于圆弧太大而无法在图中显示(阴极是通过热分解使得在透明电极上负载的铂的量发生变化)。 随着Pt量的增加,高频范围内的圆弧(在图中以ω2表示)会变小。由此可知,高频部分的圆弧是源于阴极的贡献。 另一方面,中频区域(ω3)中的圆弧不取决于铂的负载量,所以它被归结为源于阴极以外的贡献。
图20-2的下方图是用三电极系统测量的,TiO2是工作电极,对电极的影响不应该包括在内。严格来说,圆弧的顶点频率并不相同。 有一些变动。 因为频率是由电阻分量和电容分量的乘法决定的,当条件改变时,它们各自独立地受到影响。 此外,还改变溶液成分,进行了各种研究,这是一个很有意思的例子,可以很好地了解这些影响作为阻抗是如何反映出来的。 在使用性能好的对极的测量池(因为对极的阻抗会很小),2极方式的阻抗测量法也是可以的,尽管如此,3电极极式测量池的研究意义还是很大的吧。
参考文献
[20-1] K.Eguchi et al.,J.Electroanal.Chem.,588,59(2006)
第二十一篇 电化学阻抗谱(EIS)-(11)
Professor Noriyuki Watanabe
阻抗测量相对需要花费时间。 这是由于测量所需时间与频率的倒数成正比,所以频率越低,测量时间就越长。 另外还有在低频区域会有较多所需的信息。 因此,测量对象基本上没有随着时间而发生变化(恒定的),或者或者说变化很小。 如果对象的状态能基本恒定,即使有电流流动也没有关系。 如果是使用参比电极的3极方式,则只有工作电极的阻抗和未补偿溶液电阻进入测量结果。 如果将参比电极与对电极进行合并后的2极测量方式,对电极的阻抗也被包含在测量结果内。 因此,希望能尽量减小对电极的阻抗。
基于等效电路模型的分析具有多多种含义的特征。 也可以说其独特性较低。即使在不同的等效电路中,也可以获得相当接近实验结果的模拟。尽管有这样的难点,但还是因为等效电路模型分析的独特的有用性,依然在很多领域中广泛使用。因为有了之前的积累,如果能充分发挥科学的感觉,建立正确的模型也就不会很难了吧。
每种表现形式都有各自的特点。 例如,在奈奎斯特图中,虽然有不清楚频率的不便,但基本过程的分离情况一目了然,直观友好。另一方面,虽然在Bode图中可以看出阻抗的大小以及相位的变化与频率的对应关系,但由于是对数表示,很难读取细微的变化,基本过程的分离情况也容易变得不太清楚,可能存在不太容易直观观察的一面。实际上只要选择符合目的的表现形式就可以了,希望随机应变地考虑。
为了增加电极活性或催化剂活性,自然会考虑增加电极表面和催化剂表面。多孔电极是基于这样的要求而提出的,但最近涉及的领域非常广泛,包括燃料电池,电池,电容器和腐蚀。DSSC等可以说是多孔电极的终极代表类型。 在这些领域的发展进步中,对出现的现象进行分析是不可缺少的。 作为分析手段之一,电化学阻抗测量被认为是非常有用的。 至此,对于电化学阻抗的讨论到此结束。
参考文献
21-1) Tarascon et al., J.Electrochem.Soc., 148,A851,(2001) (关于锂电池)
21-2) Delacourt et al., ibid,161, A1253,(2014) (关于纽扣锂电池)
21-3) Hombrados et al., J. Power Sources 151, 25, (2005) (关于 PEMFC 的对称池)
