第十七篇 电化学阻抗谱(EIS)-(7)
Laboratory Of Research & Development, BAS Inc.
Professor Noriyuki Watanabe
Professor Noriyuki Watanabe
扩散的特殊情况 我们所考虑的扩散(Warburg扩散)是半无限一维扩散的边界条件成立的情况。 那么,当半无限一维扩散的边界条件不成立时,会出现什么情况呢? 例如,有的情况下,修饰电极中的活性物质的移动;电子和离子的移动范围受到限制,如染料敏化太阳能电池和过氧化物太阳能电池的情况;以及形成固定的扩散层,如旋转电极的情况。 这种扩散有几种不同的处理方法。 让我们分别讨论一下。
第一种称为Nernst扩散模型(Nernst diffusion, ND)。 当运动受到限制时,可称为有限扩散(finite diffusion, FD)模型。即使扩散层的厚度是有限的,但移动不受限制,旋转电极和质子交换膜型燃料电池(PEMFC)支持ND扩散。 ND的阻抗由下式给出。
第一种称为Nernst扩散模型(Nernst diffusion, ND)。 当运动受到限制时,可称为有限扩散(finite diffusion, FD)模型。即使扩散层的厚度是有限的,但移动不受限制,旋转电极和质子交换膜型燃料电池(PEMFC)支持ND扩散。 ND的阻抗由下式给出。
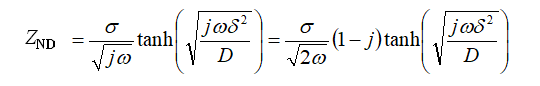
式17-1
此处的σ与Warburg阻抗(在(EIS-(4)中介绍)中的相同,取决于活性物质的浓度和扩散系数的值,随着这些值的增加,σ减小,因此阻抗也减小)。 δ对应于膜厚度。 式17-1的曲线形状受到δ2/D比率的影响,并且活性物质浓度C对σ的影响也很大,因此这些C,D和δ的变化方式复杂。 随着δ增加,直线部分变长。 当C和D降低时,扩散阻抗增加,但是C的影响更大。
此公式的模拟曲线图例如图17-1所示。(a)(b)(c)中的 Rs = 0,Rct = 8,Cdl = 10-4,D = 10-4为相同值时,可以看出当改变浓度C和膜厚度δ的参数时在奈奎斯特图中的曲线形状的变化。
此公式的模拟曲线图例如图17-1所示。(a)(b)(c)中的 Rs = 0,Rct = 8,Cdl = 10-4,D = 10-4为相同值时,可以看出当改变浓度C和膜厚度δ的参数时在奈奎斯特图中的曲线形状的变化。

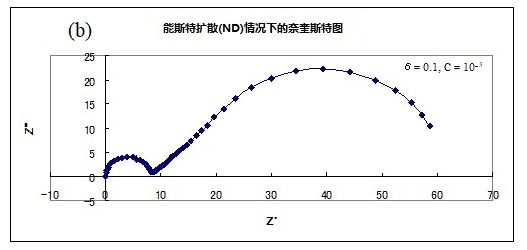
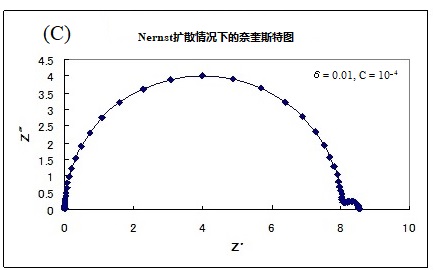
(a) δ= 0.1, C = 10-4 (b)δ= 0.1, C = 10-5 ( c) δ= 0.01, C =10-4
各图中的左侧高频侧的半圆是由于电极上的电子转移和界面双层电容的并联回路,大小不变(注意,横轴的大小不同。 它们是具有相同电阻值和相同直径的半圆形)。可以发现斜率为45°的直线的长度和随后在低频侧的弧线的大小会因膜厚度和浓度而改变。虽然只有一个电极过程,但明显出现了两条弧线。 在半无限扩散中低频侧原本是一条直线,却形成了另一个半圆。 虽然由于扩散造成的半圆比由于电极过程造成的半圆大,但它的特点也是,在低频范围内,与实轴成45度角的直线部分仍在半圆的高频侧,这就是在PEMFC和RRDE阻抗测量中经常看到的奈奎斯特图。
