第7篇 电极反应理论(2): Butler-Volmer 方程的高过电位近似和低过电位近似
从Butler-Volmer 方程(式34)中可以看到,电极反应的净电流密度是由,表示阳极电流密度的 ia 和表示阴极电流密度 ic 的两项组成。
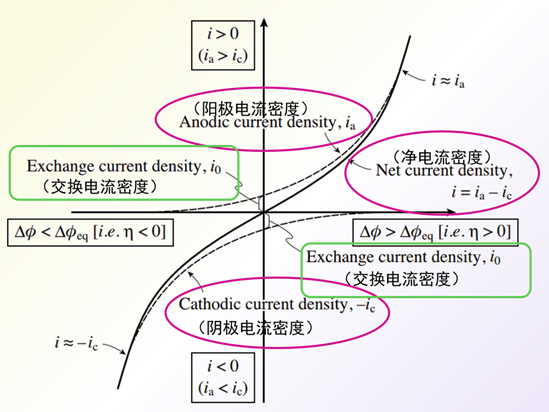
图 8 Butler-Volmer方程阳极电流密度 ia和阴极电流 密度ic(上,下虚线)和
净电流密度(实线) i =ia – ic相对于过电位 η (= Δφ – Δφeq) 的变化。
图8中的虚线表示阳极电流密度ia,阴极电流 密度ic 随过电位η的变化,为了便于区分,这里将阴极电流密度ic取负值表示。 图8中的实线表示了净电流密度i 随过电位η的变化。当η=0 时,反应处于动态平衡状态,此时的ic=ia ,用交换电流密度i0表示。
随着过电位η的增加,阳极电流密度ia增加而ic减少。 如果 η 足够大(具体而言,η> 0.10 V), 则可以忽略Butler Volmer方程中的阴极电流密度的ic项,近似处理后得到氧化反应净电流密度方程式 35。
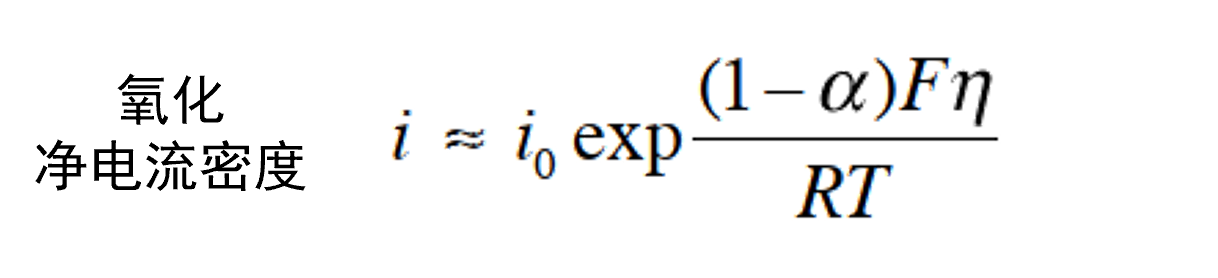
(35)
与此相反,当 η <–0.10 V 时, 则可以忽略ia 项。得到式36。
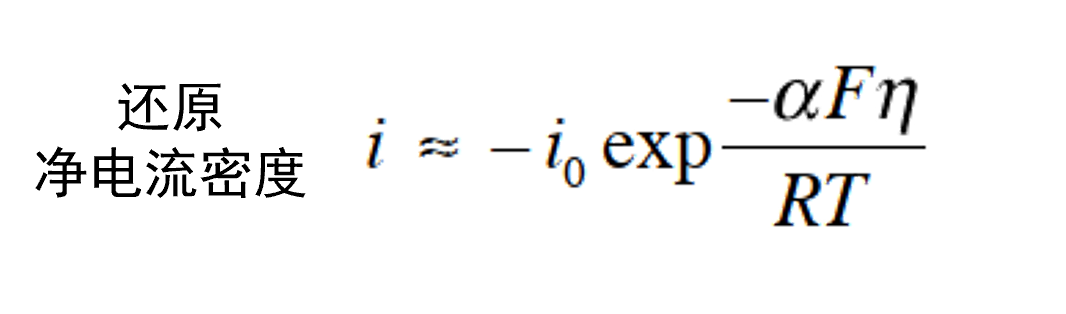
(36)
这两个方程被称为 Butler-Volmer 方程高过电位近似。
为便于作图,可将式(35)取两边的对数,变换后,得到过电位与logi 的关系式37。对于式(36),电流密度的绝对值| i | 可以用相同的方法进行处理。
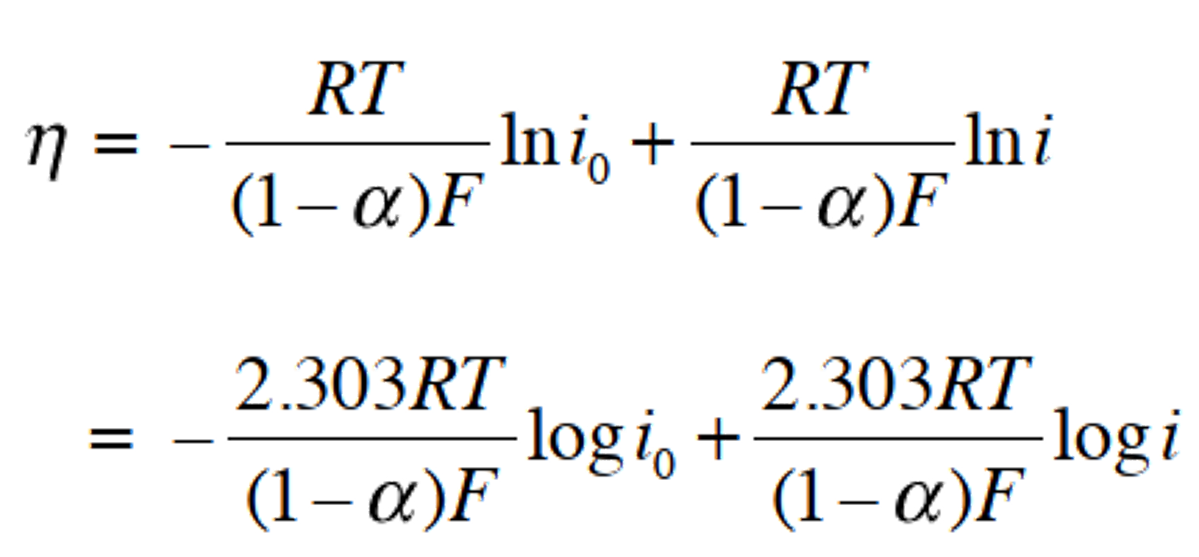
(37)

图 9 Tafel 方程的电流-电位曲线(log | i | - η ) 图 (n = 1) , 以及利用线性关系来确定 i0 和 α。
图 9表示了 η 和 log | i | 之间的关系,称为 Tafel 图。 直线部分(η <–0.10 V 和 η> 0.10 V 的部分)称为 Tafel 区域,log i0 和a值(n 电子反应情况下的 na 值)可以从这部分的截距和斜率估计。
现在的电化学,一般会将Tafel 方程(η = a ± b log | i |;a 和 b 为常数)称为 Butler-Volmer 方程的高过电位近似方程。但从历史上看,Tafel 是更早发现流过电极-电解质界面的电流与电极反应产生的过电位(电极电位)之间的关系。
考虑当过电位足够小时 (|η| <10 mV)的情况,将Butler-Volmer方程式,进行泰勒展开,并采用前两项 (expx ≈ 1+x) 得式38。
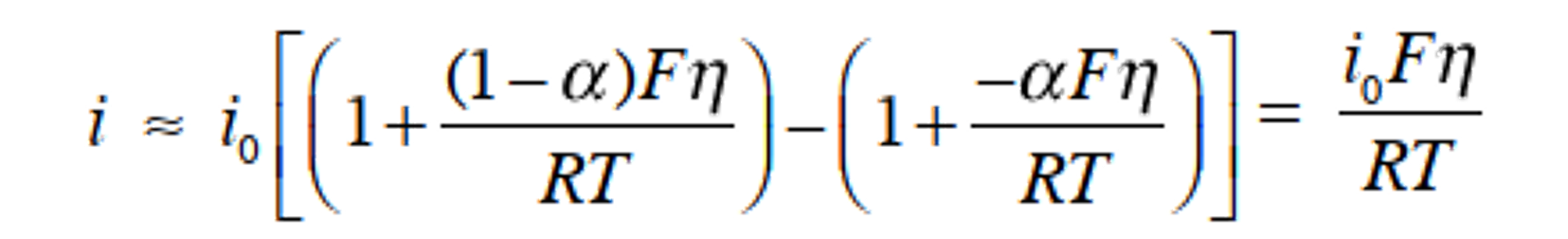
(38)
重写此式得到以下的式39。
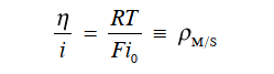
(39)
也就是说,当与平衡电位的偏差很小时(过电位很小),可以将类似于欧姆定律的东西应用于界面。式39的 比值η/i(=ρM/S)对应于界面对电极-电解质溶液界面处的电荷转移反应(也称为法拉第反应)的“电阻”,即极化电阻或电荷转移电阻)。 由于 ρM/S 主要取决于交换电流密度 i0,因此可以看作是一种“反应电阻”。 即ρM/S具有一定的电流密度(一定的电极反应速率)。它可以衡量驱动电极系统需要多少过电位的驱动力。
下面我们来看 交换电流密度 i0如何影响 η 与 i 曲线(极化曲线)。

图 10 (a) 对于三种不同的交换电流密度 ((I) i0 = 1 mA cm–2, (II) i0 = 10–3mA cm–2, (III) i0 = 10–6 mA cm–2)
Butler -Volmer方程极化曲线(n = 1,α = 0.5)和(b)图(a)中低过电位区域的放大图(注: 曲线(I) 几乎与纵轴重叠)。
图 10 (a)为 对于大中小,三种不同的交换电流密度 ((i) i0 = 1 mA cm–2, (ii) i0 = 10–3 mA cm–2, (iii) i0= 10–6mA cm–2的Butler -Volmer方程极化曲线(n = 1,传递系数α = 0.5)
将其低过电位区域的放大后表示在图10(b)中(注:曲线I 几乎与纵轴重叠)。如果 i0 变得非常大,则 ρM/S 接近于零,极化曲线平衡电位附近的梯度接近无穷大。因此,跨界面的电位差Δφ与平衡时的电位差Δφeq基本相同。这样的界面称为非极化界面。
在另一个极端情况下,i0 无限小,ρM / S 变成无限大。此时仅有非常小的电流流过界面时,电位差Δφ会与Δφeq有很大的偏差。从不同的角度来看,即使η增加一点,电化学反应也几乎不会发生。这种界面称为可极化界面。
ρM/S和i0也是电荷转移反应速率的电位大小和极性的指标。图10 就是极化曲线的形状差异取决于i0的大小示意图。用于参比电极的体系必须具有非极化界面。这是因为希望电位差Δφ能稳定在一个定值。理想情况下,用于电池等储能设备的电极系统也应具有低极性。这是因为如果 ρM / S 大,则在充电/放电过程中会损失能量。
