第五篇 光透薄层光谱电化学⟨2⟩
Nernst图的非理想行为
在理想情况下,E对lg{r(E)}的 Nernst 作图应是一条直线,很多体系都属于这种情况,但在某 些情况下,也观察到 Nernst 图偏离直线,其中的一种情况是由于在被分析的溶液中,两种或多种氧化还原物质的光谱发生重叠,并在所研究的电位范围内各光谱发生变化,其二是不同氧化还原中心的协同性或相互关联,下面将分别加以讨论。
1. 光谱上重叠的、化学上非关联的氧化还原体系
考虑溶液中同时存在几个非关联氧化还原体系,i 组分半反应的Nernst方程可以表示为
图5-1 是具有不同氧化还原计量学和光谱行为的两组分 体 系的lg{r'(E)}对E作图,为便于比较,所加电位范围和两式量 氧化还原电位集中在0mV附近,具有不同式量氧化还原电位(E1o',E2o')的影响见图5-1(A)。与所预料的一样,当 θ1=θ2 即两组分具有相同的式量电位和电子转移数,产生的Nernst图(曲线a)是具有2.303RT/AF斜率的直线,然而,当θ1不等于θ2 时,则偏离线性,两式量电位的差别越大,偏离得越明显,因此,按通常的Nernst作图,拟合这些数据(θ1=θ2 )为线性将产生E1o'和x的测量误差,图中两直线部分的延长线在y轴上的截距可分别得到两电化学氧化还原对的式量电位,每段直线区域的斜率表示每一电化学氧化还原对电子转移数。
图5-1(B)是不同电子转移计量学的影响〈 n1=1,n2 =2),尽管与上图具有相同的A应"和△A,值,但曲线的形状大不相同。按常规的Nernst作图来拟合这些模拟的响应将产生测定 值的更大偏差,由图中两线性部分的斜率和截距可以得到分别的式量电位和电子转移数。
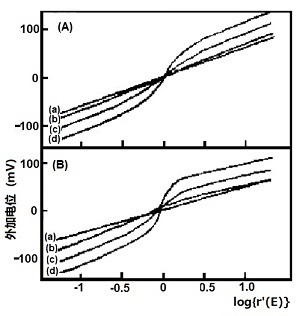
图5-1 (A)不同式量电位对模拟的Nernst图的影响。
摸拟中所用的参数为E1o'= 0 mV,E2o'=0mV(曲线a); E1o'=-25 mV,E2o'=25mV(曲线b);E1o'=-50mV,E2o'= 50 mV(曲线c); E1o'= -75 mV,E2o'= 75 mV(曲线d);n1=1,n2=1;ΔA1=1,ΔA2=1
(B) 不同电子转移计量学对模拟Nernst图的影响。
摸拟中所用的参数为E1o'= 0 mV,E2o'=0mV(曲线a); E1o'=-25 mV,E2o'=25mV(曲线b);E1o'=-50mV,E2o'= 50 mV(曲线c); E1o' = -75 mV,E2o'= 75 mV(曲线d); n1=1,n2=2,ΔA1=1,ΔA2=1 [5]
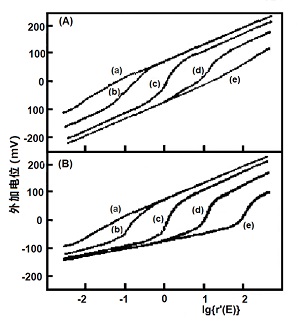
图5-1 (A)不同吸光度变化比值对模拟的Nernst图的影响。
模拟中所用的参数为E1o'= -75 mV,E2o'= 75mV;n1=1,n2=1;△A2/△A1: 100(a),10(b),1(c),1/10(d),1/100(e)
(B)不同吸光度变化比值对模拟的的Nernst图的影响。
模拟中所用的参数为EE1o'=-75mV,E2o'= 78mV;n1=1,n2=2; △A2/△A1:100(a), 10(b),1(c),1/10(d),/100(e)[5]
不同吸光度变化的比值△A2/△A1对 Nernst 图的影响见图 5-2(A),两式量电位分别为E1O'=-75mV,E2O''=75mV,电子转移数(n1=n2 =2,这些"f”形曲线的拐点取决于△A2/△A1的比值,而且当△A2/△A1项被第二(曲线a)氧化还原对(E2o'=75mV)或第一(曲线e)氧化还原对(E2o'=-75mV)控制时,Nernst图的形状主要由具有较大吸光度变化△A 的氧化还原对所控制,因此,在极限的情况下 (图5-2(A)曲线a,e),即某氧化还原电对的吸光度变化远远大于或远远小于另一氧化还原电对的吸光度变化时,以直 线 来 拟 合 Nernst 图可以较正确地确定具有较大△A 的氧化还原电对的应E1o'和n值。
在两氧化还原电位固定于0mV、n1=1、n2=2 及吸光度变化较大的情况下,模拟的 Nerrst图非常接近于一条直线,模拟数据得到的#值在1.0至2.0之间,主要取决于各氧化还原电对对总吸光度贡献的大小,式量电位非常接近于0mV。
图5-2(B)是 两 氧化还原对分别具有不同电子转移数的情况。在极限情况下, Nernst 图的斜率和截距近似于只与具有较大△A 值的氧化还原电对有关,在两者光吸收变化不大的情况下,可分别根据各渐近线的斜率和截距而求得分别的n和Eo'值。
铁氰化钾和邻甲联苯胺混合物薄层光谱电化学实验及其模拟响应如图5-3及表5-1,选择铁氰化钾和邻甲联苯胺是 因为它们可以代表光谱重叠且已被很好表征、化学上非关联的光谱电化学体系,另外,这些氧化还原对提供了评估化学非相关氧化还原体系模型有效性的方便实验对。
在两氧化还原电位固定于0mV、n1=1、n2=2 及吸光度变化较大的情况下,模拟的 Nerrst图非常接近于一条直线,模拟数据得到的#值在1.0至2.0之间,主要取决于各氧化还原电对对总吸光度贡献的大小,式量电位非常接近于0mV。
图5-2(B)是 两 氧化还原对分别具有不同电子转移数的情况。在极限情况下, Nernst 图的斜率和截距近似于只与具有较大△A 值的氧化还原电对有关,在两者光吸收变化不大的情况下,可分别根据各渐近线的斜率和截距而求得分别的n和Eo'值。
铁氰化钾和邻甲联苯胺混合物薄层光谱电化学实验及其模拟响应如图5-3及表5-1,选择铁氰化钾和邻甲联苯胺是 因为它们可以代表光谱重叠且已被很好表征、化学上非关联的光谱电化学体系,另外,这些氧化还原对提供了评估化学非相关氧化还原体系模型有效性的方便实验对。
![图5-3 亚铁氰化钾和邻联甲苯胺混合物的实验(*)及模拟(--)Nernt图&sup([5-1] 图5-3 亚铁氰化钾和邻联甲苯胺混合物的实验(*)及模拟(--)Nernt图&sup([5-1]](http://als-japan.com.cn/xdata/technical/fig5-3-thinlayer.jpg) ,
,图5-3 亚铁氰化钾和邻联甲苯胺混合物的实验(*)及模拟(--)Nernt图[5-1]
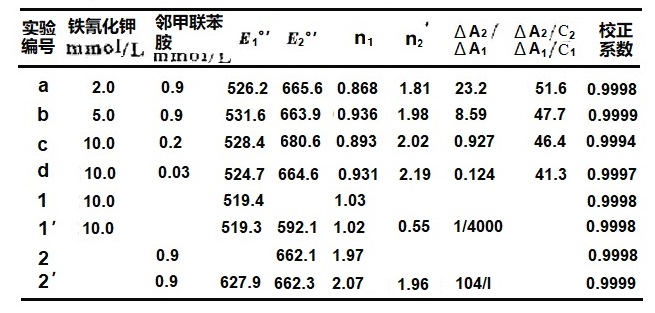
如图5-3所示,该模型与实验结果的相符性是很明显的,混合物研究中Eo'和n值的研究结果也与它们分别单独存在时的测定结果相符。邻联甲苯胺的平均式量电位 和 电 子 转 移 数为663.6±2.3mV vs.Ag/AgCl及2.02±0.19(实验a,b、c、d)与报道值659mV和1.9相符,铁氰化钾的结果也是符合的。最后,如果将单一组分存在下的实验数据按上述两组分同时存在模式来进行分析的话,占主要成分的氧化还原对的EO'和n值(表5-1,实验 1´, 2´)与按通常Nernst分析的结果(表5-1,实验1,2)是一致的,但实验1´中的E2O´和n2及实验2´中的E1O'和n1是无意义的。因此,根据混合物测得的实验数据可以得到(E1O´,n1,E2O´,n2 , △A2 /△A1)这5个变量。
参考文献
[5-1] E. W. Kristonson, D. H. Igo, R. C. Eider and W. R. Heineman, J. Electroanal. Chem.,309,61-72(1991).
