第六篇 光透薄层光谱电化学(3)
Nernst图的非理想行为
本篇继续介绍Nernst图的非理想行为的第二部分。
2. 化学上相关的氧化还原对
- 先讨论两种配体对给定氧化还原对间的竞争。
对于很多氧化还原对,氧化或还原涉及到配体 的 取 代, 因此,其式量还原电位(EO')与配体的特性有关。为了描述这种情况,考虑两种配体对给定氧化还原对的氧化形式间的竞争,两反应具有相同的电子转移计量数,在这种情况下,半反应为∶O-L1 + ne = R + L1 (6-1) 上述反应的Nernst方程为O-L2 + ne = R + L2 (6-2) E = E1O' + (RT/nF) In{CO-L1 / (C RC L1)} (6-3) 将上两式改写为E = E2O' + (RT/nF) In{CO-L2 / (C RC L2)} (6-4) CO-L1 =CR CL1 θ1(E) (6-5) 式中 CL1 和 CL2 表示自由配体的浓度,将式(6-1)与(6-2)相减,重排得两氧化态之间必然存在平衡反应CO-L2 =CR CL2 θ1(E) (6-6) 式(6-7)的反应平衡常数K可以表示为O-L1 + L2 = O- L2 + L1 (6-7) K = CO-L2 CL1 / ( CO-L1 CL2 )
= θ2(E) / θ1(E)
(6-8)大多数实验条件下,CL1 和 CL2 是大大过量的,可当做常数来处理,根据Beer定律得任意电位下总吸光度为K = exp {n(E1O' -E2O')F / RT} (6-9) 将式(6-3), (6-6),(6-8)代入式 (6-10)A(E) = (εO1CO-L1 +εO2 CO-L2 + εRCR + εL1 CL1 + εL2 CL2 ) d (6-10) A(E)=(α1 CR θ1(E) +εRCR + εL1 CL1 + εL2 CL2 ) d (6-11) 氧化还原态物质的总浓度为常数其中 α1=εO1CO-L1+ εO2 K CL2 (6-12) C* = CO-L1 + CO-L2 + CR
={α2 θ1(E) +1} CR(6-13)
(6-14)将式(6-13)代入式(6-11),得α2 = CL1 + K CL2 (6-15) 氧化态和还原态的极限吸光度可以表示为A(E)=(α1 θ1(E) +CO }C*d/ {(α2 θ1(E) +1}+ ( εL1 CL1 + εL2 CL2) d (6-16) AO = (α1 /α2)C*d + ( εL1 CL1 + εL2 CL2) d (6-17) AO = εRC*d + ( εL1 CL1 + εL2 CL2) d (6-18) 在CL1和CL2大大过量于C*的情况下,所作Nernst图仍然是线性的,但也应该看到由于式(6-30) 中等式右边多了一项,故所得截矩并不为式量电位E1O'值。ln{ r(E)} = ln (α2θ1(E)
= n (E - E1O')F /RT + ln {CL1+ K CL2 }(6-19)
(6-20)
- 再考虑含两个连续电子转移的电极过程[6-1]考虑下述可逆过程
在电位E下达平衡时,有
O ⇔ P ⇔ R (6-21) CO / CP= exp {(E - E1O' ) F/RT } (6-22) E1O'和 E2O' 分别表示O ⇔ P和P ⇔ R的式量电位,由于共总浓度保持不变CP / CR= exp {(E - E2O' ) F/RT } (6-23) 给定波长吸光度A(E)为C*= CO+ CP + CR (6-24) A(E) =d(COεO +CPεP +CR εR )
=AO+ d {CP(εP-εO ) + CR (εR -εO ) }
=AR+ d {CO(εO-εR ) + CP (εR -εO ) }(6-25)
(6-26)
(6-27)同样有 AO = dC*εO
AR = dC*εR(6-28)
(6-29)r(E) = {CO (εO -εR) + CP (εP-εR) } / {CP(εO -εP)+ CR(εO -εR)} (6-30) 将式(6-22), (6-23)代入式 (6-31),化简得r(E) =CP /CR {CO/CP (εO-εR) +εP -εR} / {CP /CR(εO-εP)+εO-εR} (6-31) 为方便起见,使用了下述无因次变量r (x)=(x/θ1δ) [x + (1-δ)θ1] /〔x+(θ2/δ)〕 (6-32) 对式 (6-32) 两边取对数x= exp(FE/ RT) ;
θ1= exp(FE1O’/RT)
θ2 = exp(FE2O’/RT)
δ = (εO-εP) + (εO-εR)(6-33)
(6-34)
(6-35)
(6-36)图6-1是使用不同θ1/θ2和δ值的几个有代表性的 Nernst图。对于δ(1-δ)>θ2/θ1 ,曲线的斜率从较小x下的1逐渐减小,通过一个极小值,然后在较大x值下增加到1,如曲线(b)和(c)所示。当δ(1-δ)<θ2/θ1 时,斜率从1增加通过一个极大值,然后减小到1,如曲线(e); 曲线(d)表示 δ(1-δ)=θ2/θ1的特 殊 情况,斜率保持不变,其值为1,对于中间体P的吸光系 数 与O的吸光系数相等的情况,δ= 0,Nernst图的斜率从较小x值的1连 续增加到较大z值时的2,如曲线(a);对于P的吸光系数等于R的吸光系数的情况即δ=1,斜率从2连续减小到1,用曲线(f)来表示。y(z) = ln{r(x)}
=lnx + ln{x+(1-δ)θ1} - In(x+θ(sub(2);/δ)-In(θ1δ )(6-37)
(6-38)![图6-1 不同[θ2 /θ1, δ ]值下的Nernst图 图6-1 不同[θ2 /θ1, δ ]值下的Nernst图](http://als-japan.com.cn/xdata/technical/sec_fig6-1.jpg)
图6-1 不同(θ2 /θ1, δ )值下的Nernst图
(a)40, 0; (b)40, 0.3; (c)20, 0.5;(d)4, 0.5;(e)2, 0.9;(f)2,1[6-1]]
图6-2显示渐近线、载矩和拐点的Nernst图
曲线(B)为式(6-39)及θ1=1,Inθ2=-3,δ=0.2,
渐近线(A)为式(6-40)及(C)为式(6-41)[6-1]上述Nernst图的斜率为dy/dlnx=1-x/[x+(1-δ)θ1]+x/[x+θ2/δ] (6-39)
因此,对于0<δ<1的情况,当x趋近于0和趋向∞时,斜率趋近于1。当x→0时,Nernst图趋近于斜率为1的渐近线当x→∞时,渐近线为yo(x)= Inx -ln{θ2/(1-δ)} (6-40) 两渐近线在水平线In{r(E)}=0上的交点分别给出x=θ2/(1-δ) 和x=θ1δ1 ,如图6-2中点a,c所示。y∞(x)=1nx-ln(θ1δ) (6-41)
通过微分式 (6-39),Nernst图的拐点b的值为 1/2ln{θ1θ2(1-δ)/δ}, ln{(1-δ)/δ}换句话说,r(x)曲线具有极值的点处的(1-δ)/δ的值斜率,即θ1θ2(1-δ)/δ 大于1时的最小斜率和θ1θ2(1-δ)/ δ最大斜率。因此,根据拐点处r(E)的实验确定值加上实验渐近线的两个截距的值(a,c),可以估算出θ1,Inθ2 和 δ的值。
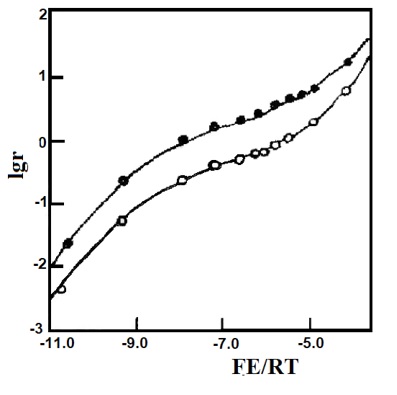
图6-3 DMF中,lmmol/L Au(squarate)2-的Nernst作图[6-1]。
使用金栅格光学透明薄层池[6-2]在(●)362 nm处,(O)364 nm处的测量值。
理论曲线根据E1O'=- 0.104V,E2O'=-0.249 V及 δ = 0.44 (上曲线)和 δ = 0.62(下曲线)得到。
图6-3是两个不同监测波 长(362nm, 364nm)下,1mM的方酸金阴离子[Au(squarate)2]-在0.5M的TEAP/DMF溶液中的Nernst图,通过实验点的 曲线由 式 (6-38)计算,E1O´=- 0.104 V,E2O´=-0.249 V及不同波长下的δ值,EO´和δ值。通过上述作图法估算,然后根据最小二乘法回归得到其精确值。
参考文献
[6-1] W.T.Yap, G.Marbung, E.A.Blubaugh and R.A.Durst, J. Elecroanal.Chem.and Interfacial Electrochem, 271, 325-329 (1989)
[6-2] E.A. Blubaugh and L.M. Doane, Anal. Chem., 54, 329-331 (1982)
